练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若直角梯形的一腰是另一腰的2倍，则这个梯形的最大角与最小角之比是

    [　　]

    A．2∶1
    B．3∶1
    C．4∶1
    D．5∶1
    答案：D
    解析：

    如图：过D作DE⊥BC于E

    ∵AD∥BE，AB∥DE，且∠A＝90°

    ∴四边形ABED是矩形

    ∴DE＝AB

    ∵CD是AB的2倍，DE⊥BC

    又∵CD＝2DE

    ∴∠C＝30°

    ∵AD∥BC

    ∴∠D+∠C＝180°

    ∴∠D＝120°

    ∴这个梯形的最大角与最小角之比是4∶1

    ∴选C


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图1、2，已知抛物线y=ax2+bx+3经过点B（-1，0）、C（3，0），交y轴于点A．
    （1）求此抛物线的解析式；
    （2）如图1，若M（0，1），过点A的直线与x轴交于点D（4，0）．直角梯形EFGH的上底EF与线段CD重合，∠FEH=90°，EF∥HG，EF=EH=1．直角梯形EFGH从点D开始，沿射线DA方向匀速运动，运动的速度为1个长度单位/秒，在运动过程中腰FG与直线AD始终重合，设运动时间为t秒．当t为何值时，以M、O、H、E为顶点的四边形是特殊的平行四边形；
    （3）如图2，抛物线顶点为K，KI⊥x轴于I点，一块三角板直角顶点P在线段KI上滑动，且一直角边过A点，另一直角边与x轴交于Q（m，0），请求出实数m的变化范围，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图1、2，已知抛物线y=ax2+bx+3经过点B（-1，0）、C（3，0），交y轴于点A．
    （1）求此抛物线的解析式；
    （2）如图1，若M（0，1），过点A的直线与x轴交于点D（4，0）．直角梯形EFGH的上底EF与线段CD重合，∠FEH=90°，EF∥HG，EF=EH=1．直角梯形EFGH从点D开始，沿射线DA方向匀速运动，运动的速度为1个长度单位/秒，在运动过程中腰FG与直线AD始终重合，设运动时间为t秒．当t为何值时，以M、O、H、E为顶点的四边形是特殊的平行四边形；
    （3）如图2，抛物线顶点为K，KI⊥x轴于I点，一块三角板直角顶点P在线段KI上滑动，且一直角边过A点，另一直角边与x轴交于Q（m，0），请求出实数m的变化范围，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年山东省泰安市九年级上学期期末考试数学试卷（解析版） 题型：解答题

    如图,抛物线y=ax2+bx+c与x轴的一个交点A的坐标为（﹣1，0），对称轴为直线x=﹣2．

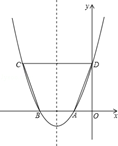
    （1）求抛物线与x轴的另一个交点B的坐标；

    （2）点D是抛物线与y轴的交点，点C是抛物线上的另一点．若以AB为一底边的梯形ABCD的面积为9．

    求此抛物线的解析式，并指出顶点E的坐标；

    （3）点P是（2）中抛物线对称轴上一动点，且以1个单位/秒的速度从此抛物线的顶点E向上运动．设点P运动的时间为t秒．

    ①当t为　  　秒时，△PAD的周长最小？当t为      秒时，△PAD是以AD为腰的等腰三角形？（结果保留根号）

    ②点P在运动过程中，是否存在一点P，使△PAD是以AD为斜边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

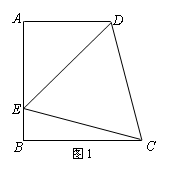
    如图1所示，在直角梯形ABCD中，AD∥BC，AB⊥BC，∠DCB=75º，以CD为一边的等边DCE的另一顶点E在腰AB上．

    （1）求∠AED的度数；

    （2）连接AC，试说明：△ABC是等腰三角形；

    （3）如图2所示，若F为线段CD上一点，∠FBC=30º．求证： DF =FC；


    查看答案和解析>>

    同步练习册答案