
已知某二次函数的图象与 轴分别相交于点
轴分别相交于点 和点
和点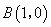 ,
,
与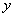 轴相交于点
轴相交于点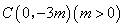 ,顶点为点
,顶点为点 。
。
⑴求该二次函数的解析式(系数用含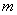 的代数式表示);
的代数式表示);
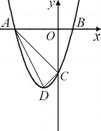
⑵如图①,当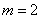 时,点
时,点 为第三象限内抛物线上的一个动点,设
为第三象限内抛物线上的一个动点,设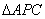 的面积为
的面积为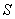 ,试求出
,试求出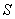 与点
与点 的横坐标
的横坐标 之间的函数关系式及
之间的函数关系式及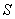 的最大值;
的最大值;
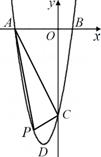
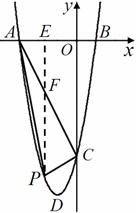
⑶如图②,当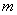 取何值时,以
取何值时,以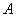 、
、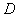 、
、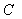 三点为顶点的三角形与
三点为顶点的三角形与 相似?
相似?
 | |||||
| |||||
| |||||
 解:⑴∵该二次函数的图象与
解:⑴∵该二次函数的图象与 轴分别相交于点
轴分别相交于点 和点
和点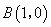 ,
,
∴设该二次函数的解析式为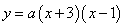
∵该二次函数的图象与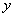 轴相交于点
轴相交于点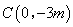 ,
,
∴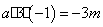 ,故
,故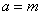
∴该二次函数的解析式为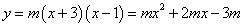
⑵当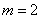 时,点
时,点 的坐标为
的坐标为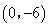 ,该二次函数的解析式为
,该二次函数的解析式为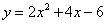
∵点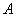 的坐标为
的坐标为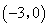 ,点
,点 的坐标为
的坐标为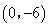
∴直线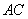 的解析式为
的解析式为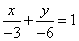 ,即
,即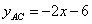
过点 作
作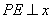 轴于点
轴于点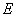 ,交
,交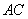 于点
于点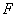
∵点 为第三象限内抛物线上的一个动点且点
为第三象限内抛物线上的一个动点且点 的横坐标为
的横坐标为
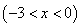
∴点 的坐标为
的坐标为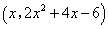 ,点
,点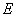 的坐标为
的坐标为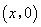 ,点
,点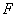 的坐标为
的坐标为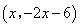
∴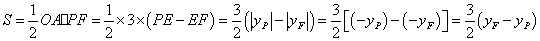
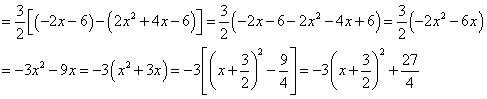
∴当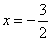 时,
时,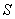 有最大值
有最大值 ;
;
另解: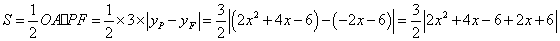
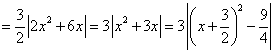
∵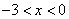 ,∴
,∴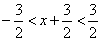 ,∴
,∴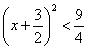 ,∴
,∴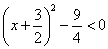 ,
,
∴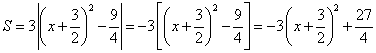 (其余略)
(其余略)
再解: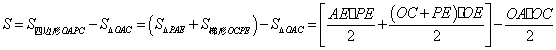
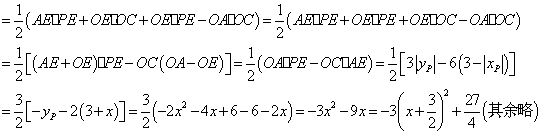
⑶∵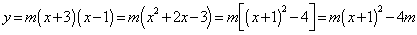 ,∴点
,∴点 的坐标为
的坐标为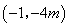
∴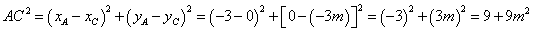
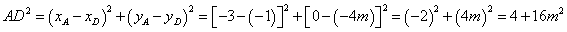
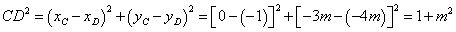
∵ 是直角三角形,∴欲使以
是直角三角形,∴欲使以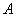 、
、 、
、 三点为顶点的三角形与
三点为顶点的三角形与 相似,必有
相似,必有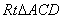
①若在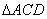 中,
中,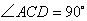 ,则
,则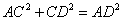 ,即
,即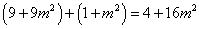
化简整理得: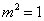 ,∵
,∵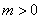 ,∴
,∴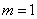 (舍去负值)
(舍去负值)
此时,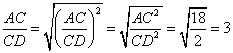 ,
,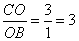 ,∴
,∴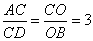
∵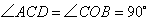 且
且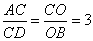 ,∴
,∴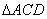 与
与 相似,符合题意;
相似,符合题意;
②若在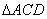 中,
中,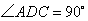 ,则
,则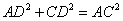 ,即
,即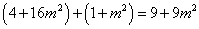
化简整理得: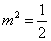 ,∵
,∵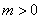 ,∴
,∴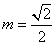 (舍去负值)
(舍去负值)
此时,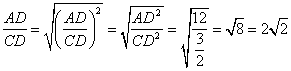 ,
,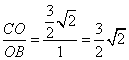 ,∴
,∴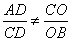
虽然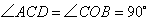 ,但是
,但是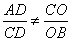 ,∴
,∴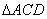 与
与 不相似,应舍去;
不相似,应舍去;
∴综上所述,只有当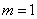 时,以
时,以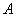 、
、 、
、 三点为顶点的三角形与
三点为顶点的三角形与 相似。
相似。


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
如图1,P(m,n)是抛物线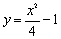 上任意一点, l是过点(0,
上任意一点, l是过点(0,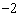 )且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
【探究】
(1)填空:当m=0时,OP= ,PH= ;当m=4时,OP= ,PH= ;
【证明】
(2)对任意m,n,猜想OP 与PH的大小关系,并证明你的猜想.
【应用】
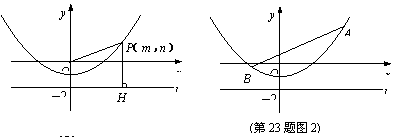
(3)如图2,已知线段AB=6,端点A,B在抛物线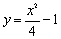 上滑动,求A,B两点到直线l的距离之和的最小值.
上滑动,求A,B两点到直线l的距离之和的最小值.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
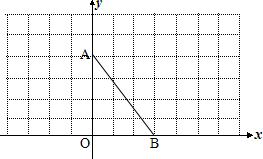
如图,在直角坐标系中,A(0,4)、C(3,0)
(1) ① 画出线段AC关于y轴对称线段AB
② 将线段CA绕点C顺时针旋转一个角,得到对应线段CD,使得AD∥x轴,请画出线段CD
(2) 若直线y=kx平分(1)中四边形ABCD的面积,请直接写出实数k的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com