
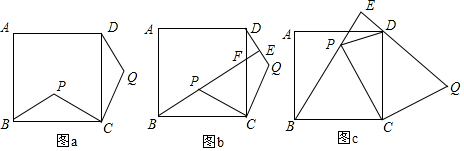
分析 (1)根据旋转的性质,证明∠BCP=∠DCQ,得到△BCP≌△DCQ;
(2)①根据全等的性质和对顶角相等,即可得到答案;②根据等边三角形的性质和旋转的性质,求出∠EPD=45°,∠EDP=45°,即可判断△DEP的形状;
(3)分两种情况进行讨论:点E在DQ上;点E在QD的延长线上,分别根据相似三角形的性质,等腰三角形的性质和勾股定理,求得BP的长即可.
解答  解:(1)证明:如图a,∵∠BCD=90°,∠PCQ=90°,
解:(1)证明:如图a,∵∠BCD=90°,∠PCQ=90°,
∴∠BCP=∠DCQ,
在△BCP和△DCQ中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCP=∠DCQ}\\{PC=QC}\end{array}\right.$,
∴△BCP≌△DCQ(SAS);
(2)①如图b,∵△BCP≌△DCQ,
∴∠CBF=∠EDF,
又∵∠BFC=∠DFE,
∴∠DEF=∠BCF=90°,
∴BE⊥DQ;
②如图c,∵△BCP为等边三角形,
∴∠BCP=60°,
∴∠PCD=30°,
又∵CP=CD,
∴∠CPD=∠CDP=75°,
又∵∠BPC=60°,∠CDQ=60°,
∴∠EPD=45°,∠EDP=45°,
∴△DEP为等腰直角三角形;
(3)如图b,由∠CBF=∠EDF,∠DEF=∠BCF,可得△DEF∽△BCF,
∴$\frac{DE}{BC}$=$\frac{DF}{BF}$,即$\frac{2}{10}$=$\frac{DF}{BF}$,
设DF=x,则BF=5x,CF=10-x,
∵Rt△BCF中,BF2=BC2+CF2,
∴(5x)2=102+(10-x)2,
解得x1=$\frac{5}{2}$,x2=-$\frac{10}{3}$(舍去),
∴BF=5x=$\frac{25}{2}$,
∵PB=PC,
∴∠PBC=∠PCB,
又∵∠PBC+∠PFC=∠PCB+∠PCF=90°,
∴∠PFC=∠PCF,
∴PF=PC,
∴BP=PF=$\frac{1}{2}$BF=$\frac{25}{4}$;
如图d,延长BE、CD,交于点F,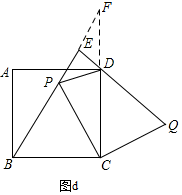
由∠CBF=∠CDQ=∠EDF,∠DEF=∠BCF,可得△DEF∽△BCF,
∴$\frac{DE}{BC}$=$\frac{DF}{BF}$,即$\frac{2}{10}$=$\frac{DF}{BF}$,
设DF=x,则BF=5x,CF=10+x,
∵Rt△BCF中,BF2=BC2+CF2,
∴(5x)2=102+(10+x)2,
解得x1=-$\frac{5}{2}$(舍去),x2=$\frac{10}{3}$,
∴BF=5x=$\frac{50}{3}$,
∵PB=PC,
∴∠PBC=∠PCB,
又∵∠PBC+∠PFC=∠PCB+∠PCF=90°,
∴∠PFC=∠PCF,
∴PF=PC,
∴BP=PF=$\frac{1}{2}$BF=$\frac{25}{3}$.
故答案为:$\frac{25}{4}$或$\frac{25}{3}$.
点评 本题属于四边形综合题,主要考查了正方形的性质、三角形全等的判定和性质、相似三角形的判定与性质、勾股定理以及旋转的性质的综合应用,掌握正方形的四条边相等、四个角都是直角,旋转的性质是解题的关键.解题时注意:旋转前后的对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
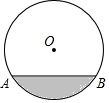 如图,水平放置的圆形管道横截面圆半径为50cm,现在水面宽度AB为60cm,当水面宽度为80cm时,则水面比原来上涨的高度为10cm或70cm.
如图,水平放置的圆形管道横截面圆半径为50cm,现在水面宽度AB为60cm,当水面宽度为80cm时,则水面比原来上涨的高度为10cm或70cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com