
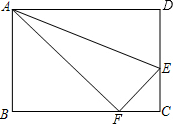
 小红用一张长方形纸片ABCD进行折纸,已知该纸片宽8,长BC为10,当小红折叠时,顶点D落在BC边上的点F处(折痕为AE),想一想,此时FC有多长?
小红用一张长方形纸片ABCD进行折纸,已知该纸片宽8,长BC为10,当小红折叠时,顶点D落在BC边上的点F处(折痕为AE),想一想,此时FC有多长? 分析 根据矩形的性质得AB=CD=8,BC=AD=10,∠B=∠C=90°,再根据折叠的性质得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC-BF=4.
解答 解:∵四边形ABCD为矩形,
∴AB=CD=8,BC=AD=10,∠B=∠C=90°,
∵长方形纸片ABCD折纸,顶点D落在BC边上的点F处(折痕为AE),
∴AF=AD=10,DE=EF,
在Rt△ABF中,AB=8,AF=10,
∴BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=6,
∴CF=BC-BF=4.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com