
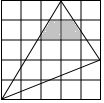
 如图,在平面内5×5的正方形网格中,每个小正方形的边长为1,则图中阴影部分面积为$\frac{107}{60}$.
如图,在平面内5×5的正方形网格中,每个小正方形的边长为1,则图中阴影部分面积为$\frac{107}{60}$. 分析 阴影部分用长方形的面积减去两个三角形列式计算即可得解.
解答 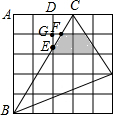 解:如图,∵△CDE∽△CAB,
解:如图,∵△CDE∽△CAB,
∴$\frac{CD}{AC}$=$\frac{DE}{AB}$,即$\frac{1}{3}$=$\frac{DE}{5}$,
∴DE=$\frac{5}{3}$,
∴EG=$\frac{2}{3}$,
同理FG=$\frac{2}{5}$,
∴阴影部分面积=2×1-$\frac{1}{3}$×$\frac{1}{2}×\frac{1}{2}$-$\frac{1}{2}$×$\frac{2}{3}$×$\frac{2}{5}$=$\frac{107}{60}$,
故答案为:$\frac{107}{60}$.
点评 本题考查了三角形的面积,根据网格结构观察出阴影部分的面积的表示是解题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
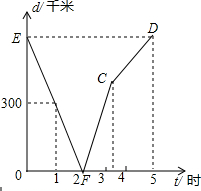 甲、乙两列火车分别从A,B两城同时相向匀速驶出,甲车开往终点B城,乙车开往终点A城,乙车比甲车早到达终点;如图,是两车相距的路程d(千米)与行驶时间t(小时)的函数关系图象.
甲、乙两列火车分别从A,B两城同时相向匀速驶出,甲车开往终点B城,乙车开往终点A城,乙车比甲车早到达终点;如图,是两车相距的路程d(千米)与行驶时间t(小时)的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | -$\frac{9}{4}$ | C. | ±$\frac{9}{4}$ | D. | -$\frac{4}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com