【题目】如图，在平面直角坐标系中， 
， 
两点的坐标分别为
， 
，连接
，若以点
， 
， 
为顶点的三角形是等腰直角三角形，则点
坐标为__________．
【答案】
， 
， 
， 
， 
， 
【解析】∵A、B两点的坐标分别为（-4，0）、（0，2）
∴OA=4，OB=2.
（1）如图，当∠APB=90°时，作PE⊥OA于点E，
易证△APE≌△BPD，则PD=PE=OE=OD，AE=BD，
设PD= 
，
则
，解得： 
，
∴此时点P的坐标为（-3，3）；
同理可得：点P1的坐标为（-1，-1）.
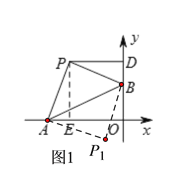
（2）如图2，当∠ABP=90°时，作PD⊥OB于点D，
易证△ABO≌△BPD，则PD=OB=2，BD=AO=4，
∴OD=OB+BD=6，
∴点P的坐标为（-2，6）.
同理可得P2的坐标为（2，-2）.
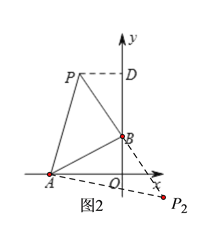
（3）如图3，过点P作PD⊥OA于点D，
易证△PDA≌△AOB，则AD=BO=2，PD=AO=4，
∴OD=AD+OA=6，
∴点P的坐标为（-6，4）.
同理可得点P3的坐标为（-2，-4）.
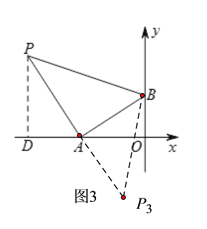
综上所述，若△PAB为等腰直角三角形，则点P的坐标为：（-3，3）、（-1，-1）、（-2，6）、（2，-2）、（-6，4）和（-2，-4）.
阳光试卷单元测试卷系列答案科目：初中数学 来源： 题型：
【题目】如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．
（1）求证：△ABQ≌△CAP；
（2）当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．
（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，直接写出它的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于实数a，我们规定：用符号
表示不大于
的最大整数，称
为a的根整数，例如： 
， 
．
（1）仿照以上方法计算： 
= ； 
= ．
（2）若
=1，写出满足题意的x的整数值 ．
如果我们对a连续求根整数，直到结果为1为止．例如：对10连续求根整数2次 
，这时候结果为1．
（3）对100连续求根整数， 次之后结果为1．
（4）只需进行3次连续求根整数运算后结果为1的所有正整数中，最大的是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题12分）从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
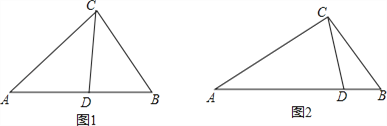
（1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．
（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且AD=CD，求∠ACB的度数．
（3）如图2，△ABC中，AC=2，BC=
，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题10分）如图，AB是⊙O的直径，BC是⊙O的弦，半径OD⊥BC，垂足为E，若BC=
，DE=3．
求：（1）⊙O的半径；（2）弦AC的长；（3）阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们学习了勾股定理后，都知道“勾三、股四、弦五”．
观察：3、4、5；5、12、13；7、24、25；9、40、41；…，发现这些勾股数的勾都是奇数，且从3起就没有间断过．
（1）请你根据上述的规律写出下一组勾股数：________．
（2）若第一个数用字母n（n为奇数，且n≥3）表示，那么后两个数用含n的代数式分别表示为________和________，请用所学知识说明它们是一组勾股数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】点
的坐标为
，点
的坐标为
，点
的坐标为
．
（
）在
轴上是否存在点
，使
为等腰三角形，求出点
坐标．
（
）在
轴上方存在点
，使以点
， 
， 
为顶点的三角形与
全等，画出
并请直接写出点
的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com