
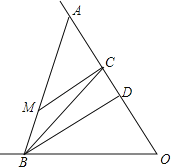
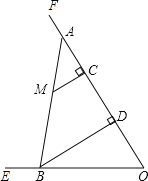
【题目】如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.

(1)当AC的长度为多少时,△AMC和△BOD相似;
(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;
(3)连结BC.当S△AMC=S△BOC时,求AC的长.
【答案】(1)2或8;(2)直角三角形,理由见解析;(3)18;
【解析】
试题分析:(1)由于∠MCA=∠BDO=Rt∠,所以△AMC和△BOD相似时分两种情况:①△AMC∽△BOD;②△AMC∽△OBD.则两种情况都可以根据相似三角形对应边的比相等及tan∠EOF=2列出关于AC的方程,解方程即可求出AC的长度;
(2)先由MC∥BD,得出△AMC∽△ABD,根据相似三角形对应边的比相等及三角形中位线的性质求出BD=2MC=8,OD=4,CD=8,AC=CD=8,再利用SAS证明△AMC≌△BOD,得到∠CAM=∠DBO,根据平行线的性质及三角形内角和定理求出∠ABO=90°,进而得出△ABO为直角三角形;
(3)设OD=a,根据tan∠EOF=2得出BD=2a,由三角形的面积公式求出S△AMC=2AC,S△BOC=12a,根据S△AMC=S△BOC,得到AC=6a.由△AMC∽△ABD,根据相似三角形对应边的比相等列出关于a的方程,解方程求出a的值,进而得出AC的长.
解:(1)∵∠MCA=∠BDO=Rt∠,
∴△AMC和△BOD中,C与D是对应点,
∴△AMC和△BOD相似时分两种情况:
①当△AMC∽△BOD时,![]() =tan∠EOF=2,
=tan∠EOF=2,
∵MC=4,
∴![]() =2,
=2,
解得AC=8;
②当△AMC∽△OBD时,![]() =tan∠EOF=2,
=tan∠EOF=2,
∵MC=4,
∴![]() =2,
=2,
解得AC=2.
故当AC的长度为2或8时,△AMC和△BOD相似;
(2)△ABO为直角三角形.理由如下:
∵MC∥BD,
∴△AMC∽△ABD,
∴![]() ,∠AMC=∠ABD,
,∠AMC=∠ABD,
∵M为AB中点,
∴C为AD中点,BD=2MC=8.
∵tan∠EOF=2,
∴OD=4,
∴CD=OC﹣OD=8,
∴AC=CD=8.
在△AMC与△BOD中,
 ,
,
∴△AMC≌△BOD(SAS),
∴∠CAM=∠DBO,
∴∠ABO=∠ABD+∠DBO=∠AMC+∠CAM=90°,
∴△ABO为直角三角形;
(3)连结BC,设OD=a,则BD=2a.
∵S△AMC=S△BOC,S△AMC=![]() AC
AC![]() MC=2AC,S△BOC=
MC=2AC,S△BOC=![]() OC
OC![]() BD=12a,
BD=12a,
∴2AC=12a,
∴AC=6a.
∵△AMC∽△ABD,
∴![]() ,即
,即![]() ,
,
解得a1=3,a2=﹣![]() (舍去),
(舍去),
∴AC=6×3=18.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】为有效开展阳光体育活动,云洱中学利用课外活动时间进行班级篮球比赛,每场比赛都要决出胜负,每队胜一场得2分,负一场得1分.已知九年级一班在8场比赛中得到13分,问九年级一班胜、负场数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想从“天猫”某网店购买计算器,经査询,某品牌A号计算器的单价比B型号计算器的单价多10元,5台A型号的计算器与7台B型号的计算器的价钱相同,问A、B两种型号计算器的单价分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中真命题有( )
①点到直线的垂线段叫做点到直线的距离;②内错角相等;③两点之间线段最短;④过一点有且只有一条直线与已知直线平行;⑤在同一平面内,若两条直线都与第三条直线垂直,则这两条直线互相平行.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.

(1)求证:①△ABG≌△AFG; ②求GC的长;
(2)求△FGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一只不透明的盒子里有背面完全相同,正面上分别写有数字1、2、3、4的四张卡片,小马从中随机地抽取一张,把卡片上的数字作为被减数;在另一只不透明的盒子里将形状、大小完全相同,分别标有数字1、2、3的三个小球混合后,小虎从中随机地抽取一个,把小球上的数字做为减数,然后计算出这两个数的差.
(1)请你用画树状图或列表的方法,求这两数差为0的概率;
(2)小马与小虎做游戏,规则是:若这两数的差为非正数,则小马赢;否则小虎赢.你认为该游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4![]() ,CQ=10,则正方形ABCD的面积为 .
,CQ=10,则正方形ABCD的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有( )
A.103块 B.104块 C.105块 D.106块
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com