
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线BC的解析式为y=﹣x+6.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线BC的解析式为y=﹣x+6.
(1)求抛物线的解析式;
(2)点M为线段BC上方抛物线上的任意一点,连接MB,MC,点N为抛物线对称轴上任意一点,当M到直线BC的距离最大时,求点M的坐标及MN+NB的最小值;
(3)在(2)中,点M到直线BC的距离最大时,连接OM交BC于点E,将原抛物线沿射线OM平移,平移后的抛物线记为y′,当y′经过点M时,它的对称轴与x轴的交点记为H.将△BOE绕点B逆时针旋转60°至△BO1E1,再将△BO1E1沿着直线O1H平移,得到△B1O2E2,在平面内是否存在点F,使以点C,H,B1,F为顶点的四边形是以B1H为边的菱形.若存在,直接写出点B1的横坐标;若不存在,请说明理由.

【答案】(1)y=﹣![]() x2+2x+6;(2)点M的坐标及MN+NB的最小值分别为:(3,
x2+2x+6;(2)点M的坐标及MN+NB的最小值分别为:(3,![]() ),
),![]() ;(3)存在,此时,点B1的横坐标为18.
;(3)存在,此时,点B1的横坐标为18.
【解析】
(1)直线BC的解析式为y=-x+6,则B(6,0)、C(0,6),把B、C坐标代入二次函数表达式,解得:y=-![]() x2+2x+6;
x2+2x+6;
(2)设M横坐标为t,则M到直线BC的距离为d=![]() =
=![]() ;点B关于对称轴的对称点为A,则AM为MN+NB的最小值,即可求解;
;点B关于对称轴的对称点为A,则AM为MN+NB的最小值,即可求解;
(3)OM所在直线方程为:y=![]() x,当抛物线沿OM直线平移时,设顶点向右平移2m,则向上平移了5m,新顶点坐标为(2+2m,8+5m),则y′=-
x,当抛物线沿OM直线平移时,设顶点向右平移2m,则向上平移了5m,新顶点坐标为(2+2m,8+5m),则y′=-![]() (x-2-2m)2+(8+5m),把点M(3,
(x-2-2m)2+(8+5m),把点M(3,![]() )代入上式,解得:m=
)代入上式,解得:m=![]() ,则H(9,0).①假设:平行四边形处于CF′HB′1位置时,该四边形为菱形,则B′1的y坐标为6,则其x坐标为9+2
,则H(9,0).①假设:平行四边形处于CF′HB′1位置时,该四边形为菱形,则B′1的y坐标为6,则其x坐标为9+2![]() ,而B′1C=9+2
,而B′1C=9+2![]() ,B′1H=4
,B′1H=4![]() ,即:B′1C≠B′1H,CF′HB′1不是菱形;②假设:平行四边形处于CHB1F位置时,该四边形为菱形,则B1的横坐标为2OH=18.
,即:B′1C≠B′1H,CF′HB′1不是菱形;②假设:平行四边形处于CHB1F位置时,该四边形为菱形,则B1的横坐标为2OH=18.
(1)直线BC的解析式为y=﹣x+6,则B(6,0)、C(0,6),
把点B、C坐标代入二次函数表达式,
解得:y=﹣![]() x2+2x+6,
x2+2x+6,
此时,顶点坐标为(2,8),A(﹣2,0);
(2)设M横坐标为t,则M到直线BC的距离为d=![]() =
=![]() ,
,
∴当t=3时,d最大,则M(3,![]() ),
),
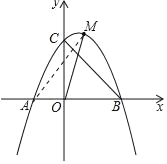
点B关于对称轴的对称点为A,则AM为MN+NB的最小值,AM=![]() =
=![]() ;
;
∴点M的坐标及MN+NB的最小值分别为:(3,![]() ),
),![]() ;
;
(3)OM所在直线方程为:y=![]() x,
x,
当抛物线沿OM直线平移时,设顶点向右平移2m,则向上平移了5m,新顶点坐标为(2+2m,8+5m),
则y′=﹣![]() (x﹣2﹣2m)2+(8+5m),
(x﹣2﹣2m)2+(8+5m),
把点M(3,![]() )代入上式,解得:m=
)代入上式,解得:m=![]() ,(m=0舍去),则H(9,0),
,(m=0舍去),则H(9,0),
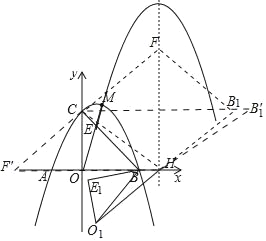
△BOE绕点B逆时针旋转60°至△BO1E1,此时,直线BO1的k值为![]() ,
,
再将△BO1E1沿着直线O1H平移,得到△B1O2E2,直线B1H的k也为![]() ,
,
则B1H所在的直线方程为:y=![]() x﹣9
x﹣9![]() ,
,
①假设:平行四边形处于CF′HB′1位置时,该四边形为菱形,则B′1的y坐标为6,则其x坐标为9+2![]() ,
,
而B′1C=9+2![]() ,B′1H=4
,B′1H=4![]() ,即:B′1C≠B′1H,CF′HB′1不是菱形;
,即:B′1C≠B′1H,CF′HB′1不是菱形;
②假设:平行四边形处于CHB1F位置时,该四边形为菱形,则B1的横坐标为2OH=18.
故:存在,此时,点B1的横坐标为18.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】某种蔬菜每千克售价![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图1所示,每千克成本
之间的关系如图1所示,每千克成本![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出![]() 与
与![]() 之间满足的函数表达式,并直接写出
之间满足的函数表达式,并直接写出![]() 的取值范围;
的取值范围;
(2)求出![]() 与
与![]() 之间满足的函数表达式;
之间满足的函数表达式;
(3)设这种蔬菜每千克收益为![]() 元,试问在哪个月份出售这种蔬菜,
元,试问在哪个月份出售这种蔬菜,![]() 将取得最大值?并求出此最大值.(收益=售价-成本)
将取得最大值?并求出此最大值.(收益=售价-成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距300千米,甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留1小时后,速度不变,按原路返回.设两车行驶的时间是x小时,离开A地的距离是y千米,如图是y与x的函数图象.
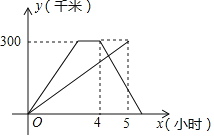
(1)甲车的速度是 ,乙车的速度是 ;
(2)甲车在返程途中,两车相距20千米时,求乙车行驶的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的各边分别平行于
的各边分别平行于![]() 轴或
轴或![]() 轴,甲乙分别由
轴,甲乙分别由![]() 点同时出发,沿矩形
点同时出发,沿矩形![]() 的边作环绕运动甲按逆时针方向以
的边作环绕运动甲按逆时针方向以![]() 个单位/秒的速度匀速运动,乙按顺时针方向以
个单位/秒的速度匀速运动,乙按顺时针方向以![]() 个单位/秒的速度匀速运动,则甲、乙运动后的第
个单位/秒的速度匀速运动,则甲、乙运动后的第![]() 次相遇地点的坐标是( )
次相遇地点的坐标是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂要招聘甲、乙两种工种的工人![]() 人,甲、乙两种工种的工人的月工资分别为
人,甲、乙两种工种的工人的月工资分别为![]() 元和
元和![]() 元
元
![]() 设招聘甲种工种工人
设招聘甲种工种工人![]() 人,工厂付给用、乙两种工种的工人工资共
人,工厂付给用、乙两种工种的工人工资共![]() 元,写出
元,写出![]() (元)与
(元)与![]() (人)的函数关系式;
(人)的函数关系式;
![]() 现要求招聘的乙种工种的人数不少于甲种工种人数的
现要求招聘的乙种工种的人数不少于甲种工种人数的![]() 倍,问甲、乙两种工种各招聘多少人时,可使得每月所付的工资最少?
倍,问甲、乙两种工种各招聘多少人时,可使得每月所付的工资最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读一段文字,再回答下列问题:已知在平面内两点的坐标为![]() ,
,![]() ,则该两点间距离公式为
,则该两点间距离公式为![]() .同时,当两点在同一坐标轴上或所在直线平行于
.同时,当两点在同一坐标轴上或所在直线平行于![]() 轴、平行于
轴、平行于![]() 轴时,两点间的距离公式可化简成
轴时,两点间的距离公式可化简成![]() 与
与![]() .
.
(1)若已知两点![]() ,
,![]() ,试求
,试求![]() 两点间的距离;
两点间的距离;
(2)已知点![]() 在平行于
在平行于![]() 轴的直线上,点
轴的直线上,点![]() 的纵坐标为7,点
的纵坐标为7,点![]() 的纵坐标为
的纵坐标为![]() ,试求
,试求![]() 两点间的距离;
两点间的距离;
(3)已知一个三角形各顶点的坐标为![]() ,
,![]() ,
,![]() ,你能判定这三点是否共线?若共线请说明理由,若不共线请求出图形的面积.
,你能判定这三点是否共线?若共线请说明理由,若不共线请求出图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
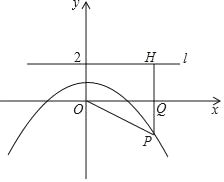
【题目】如图,P(m,n)是抛物线y=﹣![]() +1上任意一点,l是过点(0,2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H,PH交x轴于Q.
+1上任意一点,l是过点(0,2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H,PH交x轴于Q.
(1)(探究)填空:当m=0时,OP= ,PH= ;当m=4时,OP= ,PH= .
(2)(证明)对任意m,n,猜想OP与PH的大小关系,并证明你的猜想.
(3)(应用)当OP=OH,且m≠0时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
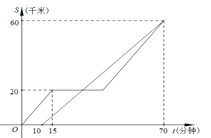
【题目】甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离S(千米)与时间t(分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:
(1)甲、乙两车行驶时的速度分别为多少?
(2)乙车出发多少分钟后第一次与甲车相遇?
(3)甲车中途因故障停止行驶的时间为多少分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com