
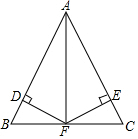
 已知:如图,△ABC中,AB=AC,FD⊥AB于点D,FE⊥AC于点E,FD=FE.求证:AF是BC的中垂线.
已知:如图,△ABC中,AB=AC,FD⊥AB于点D,FE⊥AC于点E,FD=FE.求证:AF是BC的中垂线. 分析 根据HL证得Rt△AFD≌Rt△AFE,则可得∠AFB=∠CAF,可得AF是△ABC的角平分线,然后由三线合一,证得AD是BC的中垂线.
解答 证明:∵FD⊥AB于点D,FE⊥AC于点E,
∴△AFD和△AFE是直角三角形,
在Rt△AFD和Rt△AFE中,
$\left\{\begin{array}{l}{FD=FE}\\{AF=AF}\end{array}\right.$,
∴Rt△AFD≌Rt△AFE(HL),
∴∠AFB=∠CAF,
∵AF是△ABC的角平分线,
∴AF是BC的中垂线.
点评 此题考查了等腰三角形的性质与判定以及全等三角形的判定与性质.注意掌握三线合一性质的应用.


科目:初中数学 来源: 题型:解答题
 寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如表:
寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如表:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
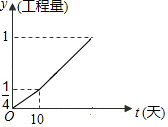 甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程,设工程总量为1,后期总工程量y与天数t之间的关系为y=kx-$\frac{1}{6}$,若工程进度如图所示,则实际完成这项工程所用的时间比甲单独完成此项工作所用的时间少12天.
甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程,设工程总量为1,后期总工程量y与天数t之间的关系为y=kx-$\frac{1}{6}$,若工程进度如图所示,则实际完成这项工程所用的时间比甲单独完成此项工作所用的时间少12天.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com