
【题目】如图,已知![]() ,在
,在![]() 的角平分线
的角平分线![]() 上有一点
上有一点![]() ,将一个
,将一个![]() 角的顶点与点
角的顶点与点![]() 重合,它的两条边分别与射线
重合,它的两条边分别与射线![]() 相交于点
相交于点![]() .
.
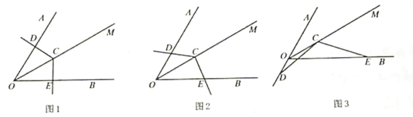
(1)如图1,当![]() 绕点
绕点![]() 旋转到
旋转到![]() 与
与![]() 垂直时,请猜想
垂直时,请猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 与
与![]() 不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)如图3,当![]() 绕点
绕点![]() 旋转到点
旋转到点![]() 位于
位于![]() 的反向延长线上时,求线段
的反向延长线上时,求线段![]() 与
与![]() 之间又有怎样的数量关系?请写出你的猜想,不需证明.
之间又有怎样的数量关系?请写出你的猜想,不需证明.
【答案】(1)![]() ,见解析;(2)结论仍然成立,见解析;(3)
,见解析;(2)结论仍然成立,见解析;(3)![]()
【解析】
(1)先判断出∠OCE=60°,再利用特殊角的三角函数得出OD=![]() OC,同OE=
OC,同OE=![]() OC,即可得出结论;
OC,即可得出结论;
(2)同(1)的方法得OF+OG=![]() OC,再判断出△CFD≌△CGE,得出DF=EG,最后等量代换即可得出结论;
OC,再判断出△CFD≌△CGE,得出DF=EG,最后等量代换即可得出结论;
(3)同(2)的方法即可得出结论.
解:(1)![]() 是
是![]() 的角平分线
的角平分线
![]()
![]()
![]()
在![]() 中,
中,![]() ,
,
同理:![]()
![]()
(2)(1)中结论仍然成立,理由:
过点![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]()
![]()
![]()
![]()
由(1)知,![]()
![]()
![]() ,且点
,且点![]() 是
是![]() 的平分线
的平分线![]() 上一点
上一点
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)结论为:![]() .
.
理由:过点C作CF⊥OA于F,CG⊥OB于G,
∴∠OFC=∠OGC=90°,
∵∠AOB=60°,
∴∠FCG=120°,
同(1)的方法得,OF=![]() OC,OG=
OC,OG=![]() OC,
OC,
∴OF+OG=![]() OC,
OC,
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,
∴CF=CG,∵∠DCE=120°,∠FCG=120°,
∴∠DCF=∠ECG,
∴△CFD≌△CGE,
∴DF=EG,
∴OF=DFOD=EGOD,OG=OEEG,
∴OF+OG=EGOD+OEEG=OEOD,
∴OEOD=![]() OC.
OC.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】探究:(1)如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2),请你写出![]() 、
、![]() 、ab之间的等量关系是______________;
、ab之间的等量关系是______________;
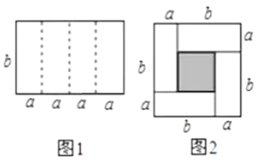
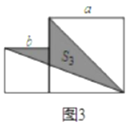
(2)两个边长分别为a和b的正方形如图放置(图3),求出图3中阴影部分的面积![]() ;
;
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC.
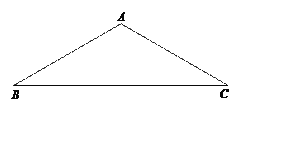
(1)用尺规作出圆心在直线BC上,且过A、C两点的⊙O;(注:保留作图痕迹,标出点O,并写出作法)
(2)若∠B=30°,求证:AB与(1)中所作⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个汽车零件制造车间可以生产甲,乙两种零件,生产4个甲种零件和3个乙种零件共获利120元;生产2个甲种零件和5个乙种零件共获利130元.
(1)求生产1个甲种零件,1个乙种零件分别获利多少元?
(2)若该汽车零件制造车间共有工人30名,每名工人每天可生产甲种零件6个或乙种零件5个,每名工人每天只能生产同一种零件,要使该车间每天生产的两种零件所获总利润超过2800元,至少要派多少名工人去生产乙种零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了解温州市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解:B.比较了解:C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题:
对雾霾的了解程度 | 百分比 | |
A | 非常了解 | 5% |
B | 比较了解 | m% |
C | 基本了解 | 45% |
D | 不了解 | n% |
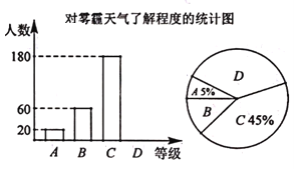
(1)本次参与调查的市民共有________人,m=________,n=________.
(2)统计图中扇形D的圆心角是________度.
(3)某校准备开展关于雾霾的知识竞赛,九(3)班郑老师欲从2名男生和1名女生中任选2人参加比赛,求恰好选中“1男1女”的概率(要求列表或画树状图).
查看答案和解析>>
科目:初中数学 来源: 题型:
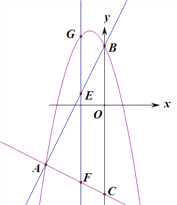
【题目】如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-![]() x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=-x2+bx+c的表达式;
(2)连接GB、EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH、HF,当点E运动到什么位置时,以A、E、F、H为顶点的四边形是矩形?求出此时点E、H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求![]() AM+CM的最小值.
AM+CM的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
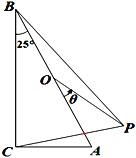
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=25°,O为AB的中点. 将OA绕点O逆时针旋转θ °至OP(0<θ<180),当△BCP恰为轴对称图形时,θ的值为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() 对称轴是直线
对称轴是直线![]() .
.
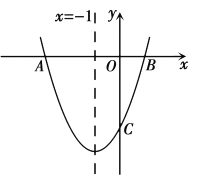
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 运动,到达点
运动,到达点![]() 即停止运动.过点
即停止运动.过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() 交线段
交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() 秒.
秒.
①连接![]() ,若
,若![]() 与
与![]() 相似,请直接写出
相似,请直接写出![]() 的值;
的值;
②![]() 能否为等腰三角形.若能,求出
能否为等腰三角形.若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com