
【题目】某商店销售面向中考生的计数跳绳,每根成本为20元,销售的前40天内的日销售量m(根)与时间t(天)的关系如表.
时间t(天) | 1 | 3 | 8 | 10 | 26 | … |
日销售量m(件) | 51 | 49 | 44 | 42 | 26 | … |
前20天每天的价格y1(元/件)与时间t(天)的函数关系式为:y1= ![]() t+25(1≤t≤20且t为整数);后20天每天的价格y2(元/件)与时间t(天)的函数关系式为:y2=﹣
t+25(1≤t≤20且t为整数);后20天每天的价格y2(元/件)与时间t(天)的函数关系式为:y2=﹣ ![]() t+40(21≤t≤40且t为整数).
t+40(21≤t≤40且t为整数).
(1)认真分析表中的数据,用所学过的一次函数,二次函数的知识确定一个满足这些数据m(件)与t(天)之间的关系式;
(2)请计算40天中娜一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<3)给希望工程,公司通过销售记录发现,前20天中扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
【答案】
(1)解:由表格中数据可知,当时间t每增加1天,日销售量相应减少1件,
∴m与t满足一次函数关系,
设m=kt+b,将(1,51)、(3,49)代入,
得: ![]() ,
,
解得: ![]() ,
,
∴m与t的函数关系为:m=﹣t+52
(2)解:设日销售利润为P,
当1≤t≤20时,
P=(﹣t+52)( ![]() t+25﹣20)=﹣
t+25﹣20)=﹣ ![]() (t﹣16)2+324,
(t﹣16)2+324,
∴当t=16时,P有最大值,最大值为324元;
当21≤t≤40时,
P=(﹣t+52)(﹣ ![]() t+40﹣20)=
t+40﹣20)= ![]() (t﹣46)2﹣18,
(t﹣46)2﹣18,
∵当t<46时,P随t的增大而减小,
∴当t=21时,P取得最大值,最大值为 ![]() (21﹣46)2﹣18=294.5元;
(21﹣46)2﹣18=294.5元;
∵324>294.5,
∴第16天时,销售利润最大,最大利润为324元
(3)解:设前20天扣除捐赠后的日利润为W,
则W=(﹣t+52)( ![]() t+25﹣20﹣a)=﹣
t+25﹣20﹣a)=﹣ ![]() [t﹣2(8+a)]2+a2﹣36a+324,
[t﹣2(8+a)]2+a2﹣36a+324,
∴对称轴为t=16+2a,
∵1≤t≤20,
∴16+2a≥20,解得:a≥2,
即a≥2时,W随t的增大而增大,
又∵a<3,
∴2≤a<3
【解析】(1)从表格可看出每天比前一天少销售1件,所以判断为一次函数关系式,待定系数法求解可得解析式;(2)日利润=日销售量×每件利润,据此分别表示前20天和后20天的日利润,根据函数性质求最大值后比较得出结论;(3)列式表示前20天中每天扣除捐赠后的日销售利润,根据函数性质求a的取值范围.


科目:初中数学 来源: 题型:
【题目】已知:△ABC中,AB=AC,∠BAC=90°.
(1)如图(1),CD平分∠ACB交AB于点D,BE⊥CD于点E,延长BE、CA相交于点F,请猜想线段BE与CD的数量关系,并说明理由.
(2)如图(2),点F在BC上,∠BFE=![]() ∠ACB,BE⊥FE于点E,AB与FE交于点D,FH∥AC交AB于H,延长FH、BE相交于点G,求证:BE=
∠ACB,BE⊥FE于点E,AB与FE交于点D,FH∥AC交AB于H,延长FH、BE相交于点G,求证:BE=![]() FD;
FD;
(3)如图(3),点F在BC延长线上,∠BFE=![]() ∠ACB,BE⊥FE于点E,FE交BA延长线于点D,请你直接写出线段BE与FD的数量关系(不需要证明).
∠ACB,BE⊥FE于点E,FE交BA延长线于点D,请你直接写出线段BE与FD的数量关系(不需要证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 是等边三角形,
是等边三角形,![]() ,
,

![]() 请你判断
请你判断![]() 的形状并说明理由;
的形状并说明理由;
![]() 如果
如果![]() 绕点
绕点![]() 旋转,交边
旋转,交边![]() 于点
于点![]() ,请你判断
,请你判断![]() 的周长是否发生变化?如果不变,说明理由;如果变化,说明当点
的周长是否发生变化?如果不变,说明理由;如果变化,说明当点![]() 在什么位置时,
在什么位置时,![]() 的周长最小.
的周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若我们规定三角“![]() ”表示为:abc;方框“
”表示为:abc;方框“![]() ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如:![]() =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
(1)计算:![]() = ______ ;
= ______ ;
(2)代数式 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;
(3)解方程:![]() =6x2+7.
=6x2+7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2 . 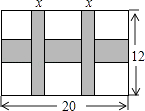
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的 ![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D. 
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点O为坐标原点,点A在x轴负半轴上,点B、C分别在x轴、y轴正半轴上,且OB=2OA,OBOC=OCOA=2.
(1)求点C的坐标;
(2)点P从点A出发以每秒1个单位的速度沿AB向点B匀速运动,同时点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动,当点Q到达终点A时,点P、Q均停止运动,设点P运动的时间为t(t>0)秒,线段PQ的长度为y,用含t的式子表示y,并写出相应的t的范围;
(3)在(2)的条件下,过点P作x轴的垂线PM,PM=PQ,是否存在t值使点O为PQ中点? 若存在求t值并求出此时△CMQ的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com