
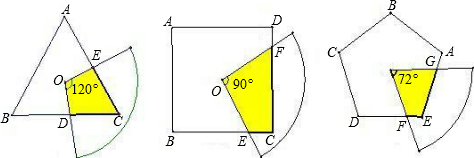

 =120°,
=120°, S△ABC=
S△ABC= S1.
S1.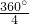 =90°,
=90°, S四边形ABCD=
S四边形ABCD= S2.
S2. S五边形ABCDE=
S五边形ABCDE= S3.
S3.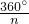 的半径足够长的扇形纸板的圆心放在边长为a面积为S的正n边形的中心O点,并将纸板绕点O旋转,正n边形的边被纸板覆盖部分的总长度为边长a,图中重叠阴影部分的面积为
的半径足够长的扇形纸板的圆心放在边长为a面积为S的正n边形的中心O点,并将纸板绕点O旋转,正n边形的边被纸板覆盖部分的总长度为边长a,图中重叠阴影部分的面积为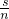 .
. S四边形ABCD=
S四边形ABCD= S2.
S2. S五边形ABCDE=
S五边形ABCDE= S3.
S3.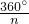 °的半径足够长的扇形纸板的圆心放在边长为a面积为S的正n边形的中心O点,并将纸板绕点O旋转,正n边形的边被纸板覆盖部分的总长度为边长a,图中重叠阴影部分的面积为
°的半径足够长的扇形纸板的圆心放在边长为a面积为S的正n边形的中心O点,并将纸板绕点O旋转,正n边形的边被纸板覆盖部分的总长度为边长a,图中重叠阴影部分的面积为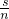 .
.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2009年山东省临沂市中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009年江苏省连云港市中考数学模拟试卷(一)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009年安徽省淮南市潘集区九年级(下)第七次联考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com