练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠CAB=70°，将△ABC绕点A逆时针旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′的度数是（ ）
    A.70°
    B.35°
    C.40°
    D.50°

    【答案】C
    【解析】解：∵△ABC绕点A逆时针旋转到△AB′C′的位置， ∴AC′=AC，∠B′AB=∠C′AC，
    ∴∠AC′C=∠ACC′，
    ∵CC′∥AB，
    ∴∠ACC′=∠CAB=70°，
    ∴∠AC′C=∠ACC′=70°，
    ∴∠CAC′=180°﹣2×70°=40°，
    ∴∠B′AB=40°，
    故选：C．
    【考点精析】本题主要考查了旋转的性质的相关知识点，需要掌握①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】计算下列各题
    （1）计算：（ ﹣2）0+（﹣1）2014+ ﹣sin45°；
    （2）先化简，再求值：（a2b+ab）÷ ，其中a= +1，b= ﹣1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在某中学第八届校园文化艺术节中，其中有三个年级老师参加的“校园歌手大奖赛”，艺术节组委会要求三个年级先进行预赛，选出男、女各一名选手参加决赛，七、八、九年级选手编号分别为男1号，女1号；男2号，女2号；男3号，女3号，比赛规则是男女各一人组成搭档进行决赛比赛．

    （1）求是同一年级男、女教师选手组成搭档的概率．

    （2）求低年级男教师与高年级女教师组成搭档的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ABC=45°，AD，BE分别为BC、AC边上的高，AD、BE相交于点F，连接CF，则下列结论：①BF=AC； ②∠FCD=45°； ③若BF=2EC，则△FDC周长等于AB的长；其中正确的有（　　）

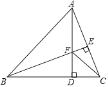
    A. 0个 B. 1个 C. 2个 D. 3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠CAB=70°，将△ABC绕点A逆时针旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′的度数是（ ）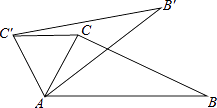
    A.70°
    B.35°
    C.40°
    D.50°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB、AC边的垂直平分线分别交BC边于点M、N．

    (1)如图①，若△AMN是等边三角形，则∠BAC=　 　°；

    (2)如图②，若∠BAC=135°，求证：BM2+CN2=MN2．

    (3)如图③，∠ABC的平分线BP和AC边的垂直平分线相交于点P，过点P作PH垂直BA的延长线于点H．若AB=4，CB=10，求AH的长．

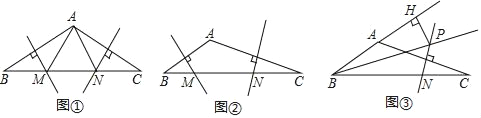
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某广告公司招标了一批灯箱加工工程，需要在规定时间内加工1400个灯箱，该公司按一定速度加工5天后，发现按此速度加工下去会延期10天完工，于是又抽调了一批工人投入灯箱加工，使工作效率提高了50%，结果如期完成工作．

    （1）求该公司前5天每天加多少个灯箱；

    （2）求规定时间是多少天．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是（ ）

    A.
    B.4
    C.
    D.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一、阅读理解：

    在△ABC中，BC=a，CA=b，AB=c；

    （1）若∠C为直角，则a2+b2=c2；

    （2）若∠C为锐角，则a2+b2与c2的关系为：a2+b2＞c2；

    （3）若∠C为钝角，试推导a2+b2与c2的关系．

    二、探究问题：在△ABC中，BC=a=3，CA=b=4，AB=c，若△ABC是钝角三角形，求第三边c的取值范围．

    查看答案和解析>>

    同步练习册答案