
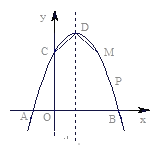
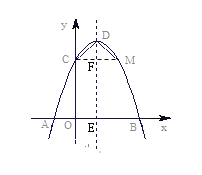
����Ŀ����ͼ����֪��������x�ύ�ڵ�A(��1��0)����y�ύ�ڵ�C(0��3)���ҶԳ��᷽��Ϊ![]() ��
��
��1������������![]() �����һ������B�����ꣻ
�����һ������B�����ꣻ
��2���������ߵĽ���ʽ��
��3���������ߵĶ���ΪD������Գ�����Ҳ�����������Ƿ���ڵ�P��ʹ�á�PDC�ǵ��������Σ������ڣ�������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��4������M����������һ�㣬��B��C��D��MΪ������ı�����ֱ�����Σ��������M�����꣮
���𰸡���1��(3,0)����2��y=-x2+2x+3����3�����ڣ����������ĵ�P����Ϊ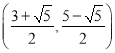 ��(2,3)����4��M(2,3)
��(2,3)����4��M(2,3)
��������
��1��������������x��Ľ���ͶԳ��᷽�̼��ɵó���������x�����һ������B������Ϊ��
(2)����A��C��B���������ô���ϵ������������������ߵĽ���ʽ��
(3)����CDΪ�ױߺ���CDΪһ����������������ۣ����ɵó���PDC�ǵ��������η��������ĵ�P�����ꣻ
(4)���ݹ��ɶ�����BCD=90�������������߶Գ��Կ�֪������MΪ(2,3).
��1������������x�ύ�ڵ�A(-1,0)���Գ��᷽��Ϊx=1��
����������x�����һ������B������Ϊ(3,0).
(2)����������y�ύ�ڵ�C(0,3)
�������߽���ʽΪy=ax2+bx+3(a������0)���������⣬��
a-b+3=0��9a+3b+3=0
���a=-1,b=2��
�������ߵĽ���ʽΪy=-x2+2x+3
(3)���ڣ�
��y=-x2+2x+3�ã�D������Ϊ(1,4),�Գ���Ϊx=1
����CDΪ�ױ�,��PD=PC,��P������Ϊ(x,y)�����ݹ��ɶ�����
x2+(3-y)2=(x-1)2+(4-y)2
��y=4-x
�ֵ�P(x,y)���������ϣ�
��4-x=-x2+2x+3��x2-3x+1=0
���![]()
![]() (��ȥ)
(��ȥ)
��![]()
��y=4-x=![]()
����P����Ϊ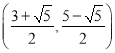 ��
��
����CDΪһ��,��Ϊ��P�ڶԳ����Ҳ����������,
�������߶Գ���֪,��P���C����ֱ��x=1�Գƣ���ʱ��P����Ϊ(2,3)
����������ĵ�P����Ϊ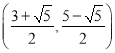 ��(2,3)��
��(2,3)��
(4)��B(3,0)��C(0,3)��D(1,4)��
���ݹ��ɶ�������CB=![]() ��CD=
��CD=![]() ��BD=
��BD=![]()
��CD2+CB2=BD2=20
���BCD=90��
��Գ��ύx���ڵ�E,��C��CM��DE,���������ڵ�M,����ΪF����ͼ��ʾ��
��Rt��DCF��
��CF=DF=1��
���CDF=45��
�������߶Գ��Կ�֪����CDM=2��45��=90����������MΪ(2,3)
��DM//BC
���ı���BCDMΪֱ������
�ɡ�BCD=90���������֪��BCΪһ��ʱ,����M���������ϵ�ֱ������ֻ������һ���������CDΪһ����BDΪһ�ף��Ҷ���M���������ϵ�ֱ�����ξ�������.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
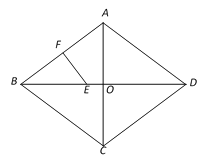
����Ŀ����ͼ����O������ABCD�Խ��ߵĽ��㣬��E��BO�ϣ�EF��ֱƽ��AB������ΪF��
��1����֤����BEF �ס�DCO��
��2����AB=10��AC=12�����߶�EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ü����ģ�����Ͷ��һöͼ����ij��ʵ��Ľ���������������ƶϣ���ij��ʵ��Ͷ��������500���������¼���������ϡ��Ĵ�����308����ô����顰�������ϡ���Ƶ����0.616��������ʵ����������ӣ����������ϡ���Ƶ������0.618�����ڶ�����ʾ��һ�����ȶ��ԣ����Թ��ơ��������ϡ��ĸ�����0.618�������ٴ��ü����ģ��ʵ�飬��Ͷ������Ϊ1000ʱ�����������ϡ��ĸ���һ����0.620�����к������ǣ�������

A. �٢� B. �ڢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AB����O��ֱ����CD����O���ң���ABD��58�㣬���BCD����������

A.116��B.32��C.58��D.64��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˶�ѧ�����и�����ͳ������������ѧ��չ�ˡ������ڼ�ɨ�����ȫУѧ����ѧУͬʱ����������![]() ������ʿ����ݣ�ѧУҪ���
������ʿ����ݣ�ѧУҪ���![]() ����ǰ����Ŀ�ĵأ����û�������������߹����У��ţ�1���ಽ�е�ƽ���ٶ����������
����ǰ����Ŀ�ĵأ����û�������������߹����У��ţ�1���ಽ�е�ƽ���ٶ����������![]() �����������������ǰ
�����������������ǰ![]() ���ӵ���ֱ���ţ�1���ࡢ�����ಽ�е�ƽ���ٶȣ�
���ӵ���ֱ���ţ�1���ࡢ�����ಽ�е�ƽ���ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
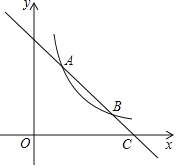
����Ŀ����ͼ��һ�κ���y����x+3��ͼ���뷴��������y��![]() ��k��0���ڵ�һ����ͼ����A(1��a)��B���㣬��x�ύ�ڵ�C��
��k��0���ڵ�һ����ͼ����A(1��a)��B���㣬��x�ύ�ڵ�C��
��1�����������Ľ���ʽ����A�����ꣻ
��2������PΪx����һ�㣬�������ACP�ǵ��������Σ���ֱ��д���������������е�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ijˮ����˾��3Ԫ/kg�ijɱ����½�10000kg���٣������˾ϣ�����������ܻ������6000Ԫ����֪��������ͳ�Ʊ����£�������д���һ�����ݣ���ɴ˱���
(1)���ʵĸ���Լ�Ƕ��٣���˵������ (����С�����һλ)
(2)�ڳ��۸���(ȥ���ĸ���)ʱ��ȷ����Լ���۶��ٺ��ʣ�
���������� | �������� | ������Ƶ�� |
300 | 30.9 | 0.103 |
350 | 35.7 | 0.102 |
400 | 39.2 | 0.098 |
450 | 44.5 | 0.099 |
500 | 50.5 | ? |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϴֹ��Ҷ�ʹ�������¶ȣ�������������Ӣ�ȹ�������Ԥ����Ȼʹ�û����¶ȣ��H�������ּ���֮�������µĶ�Ӧ����
�����¶ȣ����� | 0 | 10 | 20 | 30 | 40 | 50 |
�����¶ȣ��H�� | 32 | 50 | 68 | 86 | 104 | 122 |
���ϱ������ƶϳ�������0�ȶ�Ӧ�������¶���_____������ijһ�¶�ʱ�����¶ȵ�ֵ���Ӧ�������¶ȵ�ֵ��ȣ�����¶�Ϊ_____����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ8��������![]() �У�
��![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() ��
��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ��
��![]() Ϊ
Ϊ![]() �е㣬
�е㣬![]() �DZ�
�DZ�![]() �ϵ�һ�����㣬��
�ϵ�һ�����㣬��![]() ����Сֵ�ǣ� ��
����Сֵ�ǣ� ��

A.10B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com