Question

某商场经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具．

（1）不妨设该种品牌玩具的销售单价为x元（x＞40），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：

销售单价（元）	x
销售量y（件）
销售玩具获得利润w（元）

（2）在（1）问条件下，若商场获得了10000元销售利润，求该玩具销售单价x应定为多少元．

（3）在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于540件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？

 

Answer 1

【答案】

解：（1）

销售单价（元）	x
销售量y（件）	1000﹣10x
销售玩具获得利润w（元）	﹣10x2+1300x﹣30000

（2）﹣10x²+1300x﹣30000=10000

解之得：x₁=50，x₂=80

答：玩具销售单价为50元或80元时，可获得10000元销售利润。

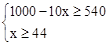（3）根据题意得，解之得：44≤x≤46 。

w=﹣10x²+1300x﹣30000=﹣10（x﹣65）²+12250

∵a=﹣10＜0，对称轴x=65，∴当44≤x≤46时，y随x增大而增大。

∴当x=46时，W_最大值=8640（元）。

答：商场销售该品牌玩具获得的最大利润为8640元。

【解析】

试题分析：（1）由销售单价每涨1元，就会少售出10件玩具得

销售量y=600﹣（x﹣40）x=1000﹣x，销售利润w=（1000﹣x）（x﹣30）=﹣10x²+1300x﹣30000。

（2）令﹣10x²+1300x﹣30000=10000，求出x的值即可；

（3）首先求出x的取值范围，然后把w=﹣10x²+1300x﹣30000转化成y=﹣10（x﹣65）²+12250，结合x的取值范围，求出最大利润。