
 其图象如下图所示.
其图象如下图所示.| 1000 |
| S |
| 1000 |
| 0.2 |
| 1000 |
| S |


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
| 5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
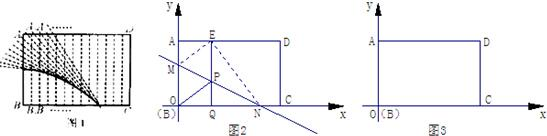
 我们知道,木板对地面的压强P(Pa)是木板面积S(m2)的反比例函数.八年级科技小组在一次实验中根据实验数据画出图象,如图所示:
我们知道,木板对地面的压强P(Pa)是木板面积S(m2)的反比例函数.八年级科技小组在一次实验中根据实验数据画出图象,如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
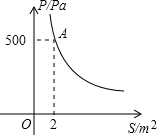 其图象如下图所示.
其图象如下图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
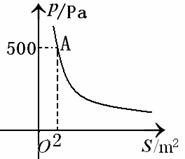
某校科技小组在一次野外考察中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木板,构筑成一条临时近道.木板对地面的压强![]() 是木板面积
是木板面积![]() 的反比例函数,其图象如下图所示.
的反比例函数,其图象如下图所示.
(1)请根据图象写出这反比例函数表达式和自变量取值范围;
(2)当木板面积为0.2m2时,压强是多少?
(3)如果要求压强不超过![]() ,木板的面积至少要多大?
,木板的面积至少要多大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com