
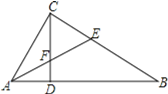
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线分别交BC、CD于E、F.
(1)求证:∠ACD=∠B
(2)求证:△CEF是等腰三角形.
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )
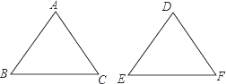
A. ∠B=∠E,BC=EF B. ∠A=∠D,BC=EF
C. ∠A=∠D,∠B=∠E D. BC=EF,AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣![]() x+
x+![]() 的图象与反比例函数y=
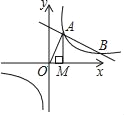
的图象与反比例函数y=![]() (k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 方格纸中小正方形的边长为1,
方格纸中小正方形的边长为1,![]() ,
,![]() 两点在格点上,要在图中格点上找到点
两点在格点上,要在图中格点上找到点![]() ,使得
,使得![]() 的面积为2,满足条件的点
的面积为2,满足条件的点![]() 有( )
有( )

A.无数个B.7个C.6个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .其中正确的结论有( )
.其中正确的结论有( )
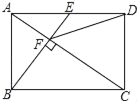
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
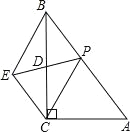
【题目】如图,在△ABC中,∠ACB=90°,AC=15.sin∠A=![]() ,点D是BC的中点,点P是AB上一动点(不与点B重合),延长PD至E,使DE=PD,连接EB、EC.
,点D是BC的中点,点P是AB上一动点(不与点B重合),延长PD至E,使DE=PD,连接EB、EC.
(1)求证;四边形PBEC是平行四边形;
(2)填空:
①当AP的值为 时,四边形PBEC是矩形;
②当AP的值为 时,四边形PBEC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com