练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图OA、AB分别表示甲、乙两名同学运动的一次函数图象，图中s和t分别表示运动路程和时间，已知甲的速度比乙快，下列说法：①射线AB表示甲的路程与时间的函数关系；②甲的速度比乙快1.5米/秒；③甲让乙先跑12米；④8秒钟后，甲超过了乙，其中正确的说法是
    ②③④
    ②③④
    （填上正确序号）．
    分析：根据函数的图象分别对每一项进行分析即可．
    解答：解：①射线AB表示乙的路程与时间的函数关系，故本选项错误，
    ②甲的速度比乙快1.5米/秒，故本选项正确，
    ③∵点B的坐标是（0，12），∴甲让乙先跑12米，故本选项正确，
    ④∵射线AB与射线OB交与（8，64），∴8秒钟后，甲超过了乙，故本选项正确，
    其中正确的说法是：②③④．
    故答案为：②③④．
    点评：此题考查了函数的图象，关键是理解函数图象横纵坐标表示的意义，通过观察图象获得必要的信息．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2013•吉林）如图①，在平面直角坐标系中，点P（0，m2）（m＞0）在y轴正半轴上，过点P作平行于x轴的直线，分别交抛物线C1：y=
    1
    4
    x2于点A、B，交抛物线C2：y=
    1
    9
    x2于点C、D．原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC和QD．
    【猜想与证明】
    填表：
    m 1 2 3
    AB
    CD
    		       
         
    由上表猜想：对任意m（m＞0）均有
    AB
    CD
    =
    2
    3
    2
    3
    ．请证明你的猜想．
    【探究与应用】
    （1）利用上面的结论，可得△AOB与△CQD面积比为
    2
    3
    2
    3
    ；
    （2）当△AOB和△CQD中有一个是等腰直角三角形时，求△CQD与△AOB面积之差；
    【联想与拓展】
    如图②过点A作y轴的平行线交抛物线C2于点E，过点D作y轴的平行线交抛物线C1于点F．在y轴上任取一点M，连接MA、ME、MD和MF，则△MAE与△MDF面积的比值为
    8
    27
    8
    27
    ．

    查看答案和解析>>

    科目：初中数学 来源：2013年吉林省高级中等学校招生考试数学 题型：047

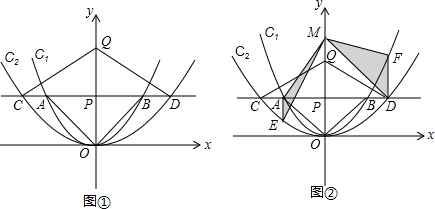
    如图①，在平面直角坐标系中，点P(0，m2)(m＞0)在y轴正半轴上，过点P作平行于x轴的直线，分别交抛物线C1：于点A、B，交抛物线C2：于点C、D原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC和QD

    猜想与证明填表：

    由上表猜想：对任意m(m＞0)均有＝________．请证明你的猜想．

    探究与应用(1)利用上面的结论，可得⊿AOB与⊿CQD面积比为________；

    (2)当⊿AOB和⊿CQD中有一个是等腰直角三角形时，求⊿CQD与⊿AOB面积之差；

    联想与拓展如图②过点A作y轴的平行线交抛物线C2于点E，过点D作y轴的平行线交抛物线C1于点F．在y轴上任取一点M，连接MA、ME、MD和MF，则⊿MAE与⊿MDF面积的比值为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图①，在平面直角坐标系中，点P（0，m2）（m＞0）在y轴正半轴上，过点P作平行于x轴的直线，分别交抛物线C1：y=数学公式x2于点A、B，交抛物线C2：y=数学公式x2于点C、D．原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC和QD．
    【猜想与证明】
    填表：
    m123
    数学公式　 　
    　　
    由上表猜想：对任意m（m＞0）均有数学公式=______．请证明你的猜想．
    【探究与应用】
    （1）利用上面的结论，可得△AOB与△CQD面积比为______；
    （2）当△AOB和△CQD中有一个是等腰直角三角形时，求△CQD与△AOB面积之差；
    【联想与拓展】
    如图②过点A作y轴的平行线交抛物线C2于点E，过点D作y轴的平行线交抛物线C1于点F．在y轴上任取一点M，连接MA、ME、MD和MF，则△MAE与△MDF面积的比值为______．

    查看答案和解析>>

    科目：初中数学 来源：2013年吉林省中考数学试卷（解析版） 题型：解答题

    如图①，在平面直角坐标系中，点P（0，m2）（m＞0）在y轴正半轴上，过点P作平行于x轴的直线，分别交抛物线C1：y=x2于点A、B，交抛物线C2：y=x2于点C、D．原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC和QD．
    【猜想与证明】
    填表：
    m123
          
         
    由上表猜想：对任意m（m＞0）均有=______．请证明你的猜想．
    【探究与应用】
    （1）利用上面的结论，可得△AOB与△CQD面积比为______；
    （2）当△AOB和△CQD中有一个是等腰直角三角形时，求△CQD与△AOB面积之差；
    【联想与拓展】
    如图②过点A作y轴的平行线交抛物线C2于点E，过点D作y轴的平行线交抛物线C1于点F．在y轴上任取一点M，连接MA、ME、MD和MF，则△MAE与△MDF面积的比值为______．

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（吉林卷）数学（解析版） 题型：解答题

    如图①，在平面直角坐标系中，点P（0，m2）（m＞0）在y轴正半轴上，过点P作平行于x轴的直线，分别交抛物线C1：于点A、B，交抛物线C2：于点C、D．原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC和QD．

    【猜想与证明】

    填表：

    m

    1

    2

    3

     

     

     

    由上表猜想：对任意m（m＞0）均有=　  　．请证明你的猜想．

    【探究与应用】

    （1）利用上面的结论，可得△AOB与△CQD面积比为　  　；

    （2）当△AOB和△CQD中有一个是等腰直角三角形时，求△CQD与△AOB面积之差；

    【联想与拓展】

    如图②过点A作y轴的平行线交抛物线C2于点E，过点D作y轴的平行线交抛物线C1于点F．在y轴上任取一点M，连接MA、ME、MD和MF，则△MAE与△MDF面积的比值为　  　．

     

     

    查看答案和解析>>

    同步练习册答案