
| 3 | a | b | c | -1 | 2 | … |
| A. | 3 | B. | 2 | C. | 0 | D. | -1 |
分析 根据三个相邻格子的整数的和相等列式求出a、c的值,再根据第9个数是2可得b=2,然后找出格子中的数每3个为一个循环组依次循环,再用2017除以3,根据余数的情况确定与第几个数相同即可得解.
解答 解:∵任意三个相邻格子中所填整数之和都相等,
∴3+a+b=a+b+c,
解得c=3,
a+b+c=b+c+(-1),
解得a=-1,
所以,数据从左到右依次为3、-1、b、3、-1、b,
第9个数与第三个数相同,即b=2,
所以,每3个数“3、-1、2”为一个循环组依次循环,
∵2017÷3=672…1,
∴第2017个格子中的整数与第1个格子中的数相同,为3,
故选:A.
点评 此题考查数字的变化规律,仔细观察排列规律求出a、b、c的值,从而得到其规律是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | (2,-3) | B. | (2,3) | C. | (3,-2) | D. | (-3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线AC=BD | B. | 四边形ABCD是平行四边形 | ||
| C. | 对角线AC⊥BD | D. | AD∥BC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
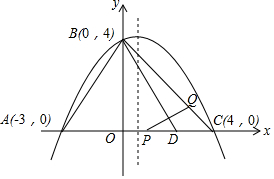 如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com