
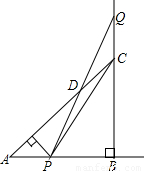
 ,而CF=AC-2AE,因此根据DE=EF+DF即可得出DE的长.
,而CF=AC-2AE,因此根据DE=EF+DF即可得出DE的长. CQ•PB.
CQ•PB. x(2-x).
x(2-x). (2x-x2)(0<x<2);
(2x-x2)(0<x<2); CQ•PB.
CQ•PB. x(x-2).
x(x-2). (x2-2x)(x>2);
(x2-2x)(x>2);
 ×2×2=2.
×2×2=2. (2x-x2)=2,即x2-2x+4=0,此方程无解;
(2x-x2)=2,即x2-2x+4=0,此方程无解; (x2-2x)=2,即x2-2x-4=0,解得x=1±
(x2-2x)=2,即x2-2x-4=0,解得x=1± .
. 时,S△PCQ=S△ABC.
时,S△PCQ=S△ABC. .
. .
. .
. -
- x,FD=
x,FD= =
= -
- x.
x. -
- x+
x+ =
= ;
; x-2
x-2 .FD=
.FD= =
= x-
x- .
. x-
x- x-(
x-( x-
x- )=
)= .
. .
.

科目:初中数学 来源:2002年全国中考数学试题汇编《图形的对称》(02)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《四边形》(02)(解析版) 题型:选择题


 +b
+b查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《三角形》(05)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2002年湖北省荆门市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com