
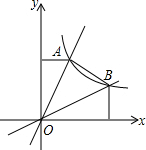
 如图,两个正比例函数y=k1x(k1>0),y=k2x(k2>0)的图象与反比例函数y=$\frac{1}{x}$的图象在第一象限分别相交于A、B两点.已知k1≠k2,OA=OB,则k1k2的值为( )
如图,两个正比例函数y=k1x(k1>0),y=k2x(k2>0)的图象与反比例函数y=$\frac{1}{x}$的图象在第一象限分别相交于A、B两点.已知k1≠k2,OA=OB,则k1k2的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 联立方程求得A、B点的坐标,然后根据OA=OB,依据勾股定理得出 $\sqrt{\frac{1}{{k}_{1}}+{k}_{1}}$=$\sqrt{\frac{1}{{k}_{2}}+{k}_{2}}$,两边平分得$\frac{1}{{k}_{1}}$+k1=$\frac{1}{{k}_{2}}$+k2,整理后得(k1-k2)(k1k2-1)=0,根据k1≠k2,则k1k2-1=0,即可求得.
解答 解:∵正比例函数y=k1x(k1>0)与反比例函数y=$\frac{1}{x}$的图象在第一象限相交于A,
∴k1x=$\frac{1}{x}$,解得x=$\sqrt{\frac{1}{{k}_{1}}}$(因为交于第一象限,所以负根舍去,只保留正根)
将x=$\sqrt{\frac{1}{{k}_{1}}}$带入y=k1x得y=$\sqrt{{k}_{1}}$,
故A点的坐标为($\sqrt{\frac{1}{{k}_{1}}}$,$\sqrt{{k}_{1}}$)同理则B点坐标为($\sqrt{\frac{1}{{k}_{2}}}$,$\sqrt{{k}_{2}}$),
又∵OA=OB,
∴$\sqrt{\frac{1}{{k}_{1}}+{k}_{1}}$=$\sqrt{\frac{1}{{k}_{2}}+{k}_{2}}$,两边平分得$\frac{1}{{k}_{1}}$+k1=$\frac{1}{{k}_{2}}$+k2,
整理后得(k1-k2)(k1k2-1)=0,
∵k1≠k2,
所以k1k2-1=0,即k1k2=1.
故选A.
点评 本题考查了反比例函数和一次函数的交点问题,解答本题的关键是运用好OA=OB这一条件,此题有一定的难度,需要同学们细心领会.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
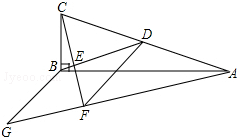 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若FG=5,CF=6,则四边形BDFG的面积为15.
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若FG=5,CF=6,则四边形BDFG的面积为15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
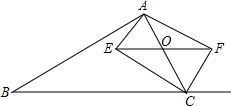 如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F
如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 用户每月用水量 | 自来水单价(元/吨) | 污水处理费用(元/吨) |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com