
分析 (1)根据待定系数法求得c,然后代入E(-2,n)即可求得E的坐标,作EM⊥x轴于M,作FN⊥x轴于N,设F(m,m2-2m-3),求得△AEM∽△FAN,根据相似三角形的性质得出$\frac{5}{1+m}$=$\frac{1}{{m}^{2}-2m-3}$,求得m的值,即可求得F的坐标;
(2)由题意可知:∠CAO=∠FOB,通过△AOC∽△ANF,得出$\frac{1}{1+m}$=$\frac{3}{{m}^{2}-2m-3}$,求得m的值,即可求得F的坐标;
(3)设F(m,m2-2m-3),直线EF的解析式为y=kx+b,代入E、F的坐标,求得b=$\frac{2{m}^{2}+m-6}{m+2}$,然后分两个情况,根据△CEF的面积等于两个三角形面积的和列出关于m的方程,解方程即可求得.
解答 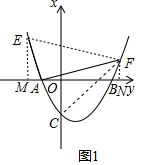 解:(1)∵抛物线y=x2-2x+c与x轴交于A(-1,0),B两点,
解:(1)∵抛物线y=x2-2x+c与x轴交于A(-1,0),B两点,
∴1+2+c=0,
解得c=-3,
∴y=x2-2x-3,
∴C(0,-3),
∵E(-2,n),F两点在抛物线上.
∴E(-2,5),
作EM⊥x轴于M,作FN⊥x轴于N,设F(m,m2-2m-3),
∵∠EAF=90°,
∴∠EAM+∠FAN=90°,
∴∠AEM=∠FAN,
∴△AEM∽△FAN,
∴$\frac{EM}{AN}$=$\frac{AM}{FN}$,即$\frac{5}{1+m}$=$\frac{1}{{m}^{2}-2m-3}$,
解得m1=$\frac{16}{5}$,m2=-1(舍去),
∴F($\frac{16}{5}$,$\frac{21}{25}$);
(2)由题意可知:∠CAO=∠FOB,如图1,
∵∠AOC=∠ANF=90°,
∴△AOC∽△ANF,
∴$\frac{OA}{AN}$=$\frac{OC}{NF}$,即$\frac{1}{1+m}$=$\frac{3}{{m}^{2}-2m-3}$,
解得m1=6,m2=-1(舍去)
∴F(6,21);
(3)设F(m,m2-2m-3),
∵E(-2,5),
设直线EF的解析式为y=kx+b,
代入F(m,m2-2m-3),E(-2,5)得$\left\{\begin{array}{l}{-2k+b=5}\\{mk+b={m}^{2}-2m-3}\end{array}\right.$
解得b=$\frac{2{m}^{2}+m-6}{m+2}$,
当b>o时,则$\frac{1}{2}$($\frac{2{m}^{2}+m-6}{m+2}$+3)(m+2)=5,
解得m=-1+$\sqrt{11}$或m=-1-$\sqrt{11}$;
∴F(-1+$\sqrt{11}$,11-4$\sqrt{11}$)或(-1-$\sqrt{11}$,11+4$\sqrt{11}$);
当b<o时,则$\frac{1}{2}$(3-$\frac{2{m}^{2}+m-6}{m+2}$)(m+2)=5,
解得m=-2或m=3;
∴F(-2,5)或(3,0);
故若△CEF的面积为5,点F的坐标为F(-1+$\sqrt{11}$,11-4$\sqrt{11}$)或(-1-$\sqrt{11}$,11+4$\sqrt{11}$)或F(-2,5)或(3,0).
点评 本题考查了抛物线与x轴的交点,三角形相似的判定和性质以及三角形面积等,作出辅助线构建相似三角形是解题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-2x | B. | y=-$\frac{2}{x}$ | C. | y=2x | D. | y=$\frac{2}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 阶梯一 | 阶梯二 | 阶梯三 |
| 月用电量230度(含)以下,每度电价0.53元 | 月用电量230度至400度(含),超过230度的部分每度比第一档提价0.05元,其他按阶梯一计算 | 月用电量400度以上,超过400度的部分每度比第一档提价0.3元,其他按阶梯一、二分别计算 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 《新闻联播》电视栏目的收视率 | B. | 一个班级学生的体重 | ||
| C. | 一批灯泡的使用寿命 | D. | 我国中小学生喜欢上数学课的人数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com