
 ��ͼ��LA��LB�ֱ��ʾA������B�ﳵ��ͬһ·����ʻ��·��S��ǧ�ף���ʱ��t��Сʱ���Ĺ�ϵ������ͼ�ش��������⣺
��ͼ��LA��LB�ֱ��ʾA������B�ﳵ��ͬһ·����ʻ��·��S��ǧ�ף���ʱ��t��Сʱ���Ĺ�ϵ������ͼ�ش��������⣺���� ��1����ͼ�Ͽɿ���B����ʱ��A���10ǧ�ף�
��2��������ʱ�����·�̲����ʱ����1.5-0.5=1Сʱ��
��3����ͼ��3Сʱʱ������ͼ���ཻ������3Сʱʱ������
��4�����B����������ʱ�Ľ���ʽ��lA�Ľ���ʽ���������ֱ�ߵĽ������꣬���ɵó��𰸣�
��� �⣺��1����ͼ�οɵ�B����ʱ��A���10ǧ�ף�
�ʴ�Ϊ��10��
��2����ͼ�з���0.5��1.5Сʱ�����г�û�����ߣ�
�ʿɵó��������õ�ʱ��Ϊ1Сʱ��
�ʴ�Ϊ��1��
��3��ͼ����ֱ�ߵĽ�����B��A������ʱ�̣�
������3Сʱ����A������
�ʴ�Ϊ��3��
��4����B����������ʱ�Ľ���ʽΪ��y=k1x����������ã�
7.5=0.5k1��
��ã�k1=15��
�����ʽΪy=15x��
��lA�Ľ���ʽΪ��y=k2x+b��
������ã�
$\left\{\begin{array}{l}{10=b}\\{22.5=3{k}_{2}+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{25}{6}}\\{b=10}\end{array}\right.$��
��lA�Ľ���ʽΪ��y=$\frac{25}{6}$x+10��
��$\left\{\begin{array}{l}{y=15x}\\{y=\frac{25}{6}x+10}\end{array}\right.$�ã�
$\left\{\begin{array}{l}{x=\frac{12}{13}}\\{y=\frac{180}{13}}\end{array}\right.$��
����A����������B�ij��������$\frac{180}{13}$ǧ�ף�
��ͼ��
�ʴ�Ϊ��$\frac{180}{13}$��
���� ���⿼��һ�κ�����Ӧ�ã��ؼ��Ǵ�ͼ���ϻ�ȡ��Ϣ������ͼ��ȷ��������ʽ���������ʽ��������֪��ȷ������ʽ���Ѷ�һ�㣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����O������AM�����ڵ�B����O�İ뾶Ϊ3������DA����OC��OA ����O�ڵ�C������BC����DA�ڵ�D��
��ͼ����O������AM�����ڵ�B����O�İ뾶Ϊ3������DA����OC��OA ����O�ڵ�C������BC����DA�ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
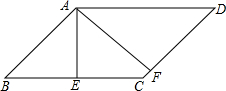 ��ͼ����ƽ���ı���ABCD�У�AE��BC��E��AF��CD��F����EAF=45�㣬��AE+AF=2$\sqrt{2}$����ƽ���ı���ABCD���ܳ��ǣ�������
��ͼ����ƽ���ı���ABCD�У�AE��BC��E��AF��CD��F����EAF=45�㣬��AE+AF=2$\sqrt{2}$����ƽ���ı���ABCD���ܳ��ǣ�������| A�� | 2 | B�� | 4$\sqrt{2}$ | C�� | 4 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�BD��CE�ֱ��ǡ�ABC�ĸߣ���BD��ȡһ��P��ʹBP=AC����CE���ӳ�����ȡһ��Q��ʹCQ=AB������AQ��AP��
��ͼ���ڡ�ABC�У�BD��CE�ֱ��ǡ�ABC�ĸߣ���BD��ȡһ��P��ʹBP=AC����CE���ӳ�����ȡһ��Q��ʹCQ=AB������AQ��AP���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com