
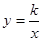 的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 .
的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 .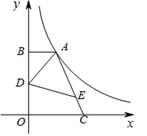
科目:初中数学 来源:不详 题型:单选题
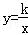 (x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )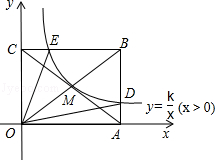
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (x>0)的图象交于点M,过M作MH⊥x,且tan∠AHO=
(x>0)的图象交于点M,过M作MH⊥x,且tan∠AHO= .
. (x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .
的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
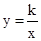 (x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示).
(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示).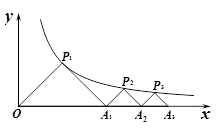
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
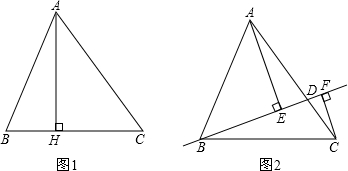
 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
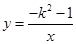 的图象上.下列结论中正确的是
的图象上.下列结论中正确的是 | A.y1>y2>y3 | B.y1>y3>y2 | C.y3>y1>y2 | D.y2>y3>y1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com