
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
分析 (1)观察第2列,由每行数之间的关系可得出依次+2、+4,用12+2+4即可求出结论;
(2)设第n行第3列的数为an,列出部分an的值,分奇偶找出变化规律“a2n+1=3(2n+1)=6n+3,a2n+2=3(2n+2)-1=6n+5”,此题得解;
(3)根据每行3个数,可找出2016在第672行,再由672为偶数即可确定2016的具体位置.
解答 解:(1)观察第2列:∵2+4=6,6+2=8,8+4=12,
∴第6行第2列的数为12+2+4=18.
(2)设第n行第3列的数为an,
观察,发现:a1=3,a2=5,a3=9,a4=11,a5=15,a6=17,…,
∴a2n+1=3(2n+1)=6n+3,a2n+2=3(2n+2)-1=6n+5(n为自然数).
(3)∵每行3个数,且2016=3×672,
∴2016在672行,
∵672为偶数,且2016为3的整数倍,
∴2016在第672行第2列.
点评 本题考查了规律型中数字的变化类,观察表格,寻找每列数的变化规律是解题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
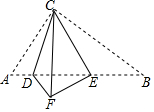 如图,在△ACB中,∠ACB=90°,∠A=45°,沿图中CD翻折,将△ACD折到△FCD,然后沿CE将△CEB翻折,使CB与CF重合,观察这个图形.
如图,在△ACB中,∠ACB=90°,∠A=45°,沿图中CD翻折,将△ACD折到△FCD,然后沿CE将△CEB翻折,使CB与CF重合,观察这个图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BC为⊙O的直径,A为圆上一点,点F为$\widehat{BC}$的中点,延长AB、AC,与过F点的切线交于D、E两点.
如图,BC为⊙O的直径,A为圆上一点,点F为$\widehat{BC}$的中点,延长AB、AC,与过F点的切线交于D、E两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com