
已知:⊙O的半径OA⊥OB,∠OAE=30°,AE交OB于D,交⊙O于E,C为OB延长线上一点,且CE=DE.求证:CE与⊙O相切.
科目:初中数学 来源: 题型:
| OD | DB |
查看答案和解析>>
科目:初中数学 来源:2010-2011学年上海市奉贤区九年级第二学期调研测试数学试卷(解析版) 题型:解答题
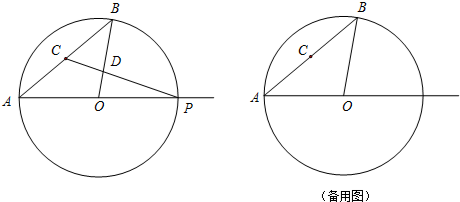
已知:⊙O的半径OA=5,弦AB=8,C是弦AB的中点,点P是射线AO上一点(与点A不重合),直线PC与射线BO交于点D.



(1)当点P在⊙O上,求OD的长.
(2)若点P在AO的延长线上,设OP=x, ,求y与x的函数关系式并写出自变量x 的取值范围。
,求y与x的函数关系式并写出自变量x 的取值范围。
(3)连接CO,若△PCO与△PCA相似,求此时BD的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com