
【题目】如图,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
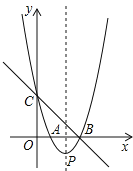
(1)求该抛物线的解析式;
(2)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)抛物线解析式为y=x2﹣4x+3;(2)Q点的坐标为(0,0)或(![]() ,0).
,0).
【解析】
试题分析:(1)先确定出点B,C坐标,再用待定系数法求函数解析式;
(2)先求出BA=2,BC=3![]() ,BP=
,BP=![]() ,然后分两种情况①由△ABC∽△PBQ,得到
,然后分两种情况①由△ABC∽△PBQ,得到![]() ,求出BQ,②由△ABC∽△QBP得
,求出BQ,②由△ABC∽△QBP得![]() ,求出BQ,即可.
,求出BQ,即可.
解:(1)∵直线y=﹣x+3与x轴、y轴分别交于点B、点C,
令x=0,得y=3,
∴C(0,3),
令y=0,得x=3,
∴B(3,0),
∵经过B、C两点的抛物线y=x2+bx+c
∴![]() ,
,
解得![]() ,
,
∴抛物线解析式为y=x2﹣4x+3;
(2)由(1),得A(1,0),连接BP,
∵∠CBA=∠ABP=45°,
∵抛物线解析式为y=x2﹣4x+3;
∴P(2,﹣1),
∵A(1,0),B(3,0),C(0,3),
∴BA=2,BC=3![]() ,BP=
,BP=![]() ,
,
当△ABC∽△PBQ时,
∴![]() ,
,
∴![]() ,
,
∴BQ=3,
∴Q(0,0),
当△ABC∽△QBP时,
∴![]() ,
,
∴![]() ,
,
∴BQ=![]() ,
,
∴Q(![]() ,0),
,0),
∴Q点的坐标为(0,0)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民选购家用净水器,一商场抓住商机,从厂家购进了A,B两种型号家用净水器,其数量和进价如表:

为使每台B型号家用净水器的售价是A型号的2倍,且保证售完这批家用净水器的利润不低于1650元,每台A型号家用净水器的售价至少应为多少元?(注:利润=售价-进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为( )
A.0.25×10-5 B.2.5×10-5 C.2.5×10-6 D.2.5×10-7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若M=(2015﹣1985)2,O=(2015﹣1985)×(2014﹣1986),N=(2014﹣1986)2,则M+N﹣2O的值为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区2014年投入教育经费2900万元,2016年投入教育经费3509万元.
(1)求2014年至2016年该地区投入教育经费的年平均增长率;
(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的增长情况,该地区到2018年需投入教育经费4250万元,如果按(1)中教育经费投入的增长率,到2018年该地区投入的教育经费是否能达到4250万元?请说明理由.
(参考数据: ![]() =1.1,
=1.1, ![]() =1.2,
=1.2, ![]() =1.3,
=1.3, ![]() =1.4)
=1.4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com