【题目】现有长度分别为3cm、4cm、5cm、8cm的4根木条
（1）李鑫同学从中任取一根，抽到“长度是4cm的木条”的概率是 ．
（2）在李鑫同学取出4cm的木条后，王华同学又从剩下的木条中，同时随机取出两根，求他们取出的三根木条能构成三角形的概率．
科目：初中数学 来源： 题型：
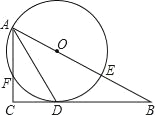
【题目】如图，在Rt△ABC中，∠C=90°，O、D分别为AB、AC上的点，经过A、D两点的⊙O分别交于AB、AC于点E、F，且BC与⊙O相切于点D．
（1）求证：
；
（2）当AC=2，CD=1时，求⊙O的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着人们生活质量的提高，净水器已经慢慢走入了普通百姓家庭，某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器，下表是近两周的销售情况：
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
（1）分别求A、B两种型号的净水器的销售单价；
（2）若该电器公司准备用不多于54000元的金额采购这两种型号的净水器共30台，求A种型号的净水器最多能采购多少台？
查看答案和解析>>
科目：初中数学 来源： 题型：
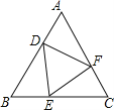
【题目】如图，在等边三角形ABC的三边上，分别取点D、E、F，使AD=BE=CF，
（1）求证：△DEF是等边三角形．
（2）若2BE=EC，求∠FEC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
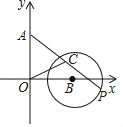
【题目】如图，在平面直角坐标系中，A（0，3）、B（3，0），以点B为圆心、2为半径的⊙B上有一动点P．连接AP，若点C为AP的中点，连接OC，则OC的最小值为（ ）
A. 1 B. 2
﹣1 C. D. 
﹣1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，点
为射线
上一个动点（不与
重合），以
为一边在的右侧作
，使
，
，过点
作
，交直线
于点
，连接
．
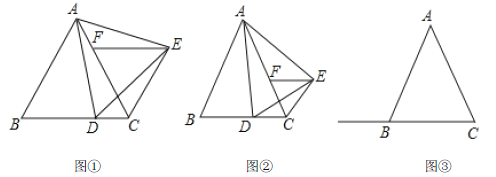
（1）如图①，若
，则按边分类：
是 三角形，并证明；
（2）若
．
①如图②，当点在线段上移动时，判断的形状并证明；
②当点在线段的延长线上移动时，是什么三角形？请在图③中画出相应的图形并直接写出结论（不必证明）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕矩形ABCD（AB＜BC）的对角线的交点O旋转（①→②→③），图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。
⑴该学习小组成员意外的发现图①（三角板一直角边与OD重合）中，BN2=CD2+CN2，在图③中（三角板一边与OC重合），CN2=BN2+CD2，请你对这名成员在图①和图③中发现的结论选择其一说明理由。
⑵试探究图②中BN、CN、CM、DN这四条线段之间的数量关系，写出你的结论，并说明理由。
⑶将矩形ABCD改为边长为1的正方形ABCD，直角三角板的直角顶点绕O点旋转到图④，两直角边与AB、BC分别交于M、N，直接写出BN、CN、CM、DM这四条线段之 间所满足的数量关系（不需要证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，△ABC 是等腰直角三角形，∠ABC=90°，AB平行x 轴，点C在 x 轴上，若点A，B分别在正比例函数 y=6x 和 y=kx 的图象上，则 k=__________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
