
����Ŀ��ij��˾�����������ӣ���ͨ���Ӽ۸���ÿ��180Ԫ��ʵľ���ӵļ۸���ÿ��400Ԫ��
(1)�ù�˾��2019���һ���������������ӹ�900�ѣ������ܽ��ﵽ��272000Ԫ�����������˸������˶��ٰѣ�
(2)�ڶ������ø������↑չ�Ҿ�չ�������˾��������ͨ����ÿ�ѽ�30Ԫ�����ۣ�ʵľ����ÿ�ѽ���2a%(a��0)�����ۣ���չ����ĵ�һ�ܣ��ù�˾����ͨ��������������һ��ȫ����ͨ���ӵ�����������![]() a%��ʵľ���ӵ��������ȵ�һ��ȫ��ʵľ���ӵ�����������a%����һ���������ӵ������۽��ﵽ��251000Ԫ����a��ֵ��
a%��ʵľ���ӵ��������ȵ�һ��ȫ��ʵľ���ӵ�����������a%����һ���������ӵ������۽��ﵽ��251000Ԫ����a��ֵ��
���𰸡���1����ͨ����������400�ѣ�ʵľ����������500�ѣ���2��a��ֵΪ15��
��������
��1������ͨ����������x�ѣ�ʵľ����������y�ѣ������ܼۣ��������������900�����ӵ������۽��Ϊ272000Ԫ�����ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ���2�����������ܼۣ����۵������������������ɵó�����a��һԪ���η��̣���֮ȡ����ֵ���ɵó����ۣ�
��1������ͨ����������x�ѣ�ʵľ����������y�ѣ�
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
����ͨ����������400�ѣ�ʵľ����������500�ѣ�
��2�������⣬�ã���180��30����400��1+![]() a%��+400��1��2a%����500��1+a%����251000��
a%��+400��1��2a%����500��1+a%����251000��
�������ã�a2��225��0��
��ã�a1��15��a2����15���������⣬��ȥ����
��a��ֵΪ15��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ҹ��Ĵ�ͳ�ѽڣ���������г�����������ϰ�ף�����ijʳƷ��Ϊ�˽������ȥ�������Ϻõ������ա���ɳ���ա��������ա��������գ����·ֱ���A��B��C��D��ʾ�������ֲ�ͬ��ζ���ӵ�ϲ��������ڽ�ǰ��ij��������������˳������飬��������������Ƴ���������ͳ��ͼ
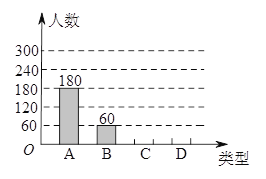
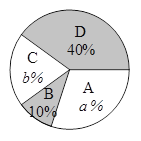
�����������Ϣ�ش�
��1�����βμӳ�������ľ�����________�ˣ�
��2������ͳ��ͼ�У�a=________��b=_________����������ͳ��ͼ����������
��3������������ȫ��ͬ��A��B��C��D�ո�һ���������С���������������б�����״ͼ�ķ����������ڶ����Ե���ǡ����C�յĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������![]() �У�
��![]() ��
��![]() �ǶԽ���
�ǶԽ���![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() ��
��![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() .
.
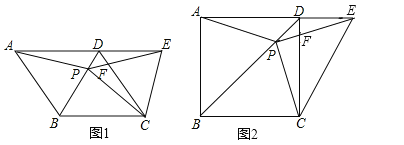
��1��֤����![]() ��
��
��2���ж�![]() ����״����˵������.
����״����˵������.
��3����ͼ2��������![]() ��Ϊ������
��Ϊ������![]() �������������䣬ֱ��д���߶�
�������������䣬ֱ��д���߶�![]() ���߶�
���߶�![]() ��������ϵ.
��������ϵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˽�ѧ��ÿ����ɼ�ͥ��ҵ����ʱ�������������ȡ�˲���ѧ�����е��飬�����������ݽ�������������������ͳ��ͼ������ͳ��ͼ���£�
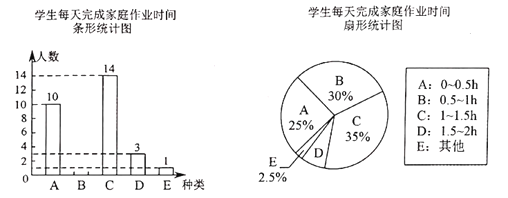
��1������ͳ��ͼ������![]() ��Բ�ĽǵĶ���Ϊ______
��Բ�ĽǵĶ���Ϊ______![]() ��
��
��2����ȫ����ͳ��ͼ��
��3��������ѧ��2000��ѧ����������ж�����ѧ������1.5Сʱ������ɼ�ͥ��ҵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
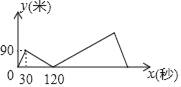
����Ŀ���ס���������1200�׳���ֱ�ߵ�·���ܲ����ס�������ͬ��㡢ͬ������������ֱ��Բ�ͬ���ٶ�����ǰ������֪���׳���30����ҳ������ҵ��յ���������أ�����ԭ�����ٶ�ǰ������������������ʱ�ܲ���������ͼ��y���ף���ʾ�ס�������֮��ľ��룬x���룩��ʾ�׳�����ʱ�䣬ͼ���������ݱ�ʾ�����ܲ�������y��x������ϵ����ô���ҵ����յ��_____�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽���������ȡ���ŵ�����Ҫ;����ij�м��߿�չ��һ�γ������飬���ݵ����������������в�������ͳ��ͼ��
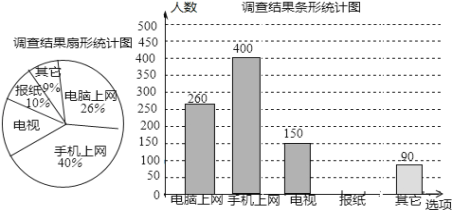
����������Ϣ����������⣺
��1����ν��ܵ������������������ �����벹ȫ����ͳ��ͼ��
��2������ͳ��ͼ�У�������������Ӧ��Բ�ĽǵĶ����� ��
��3��������Լ��90���ˣ�����������н������Ժ��ֻ���������Ϊ����ȡ���ŵ�����Ҫ;��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��ƽ�����ཻ�ڵ�
��ƽ�����ཻ�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() �����������ĸ����ۣ�
�����������ĸ����ۣ�
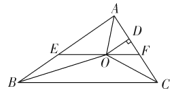
����![]() ��
��![]() ��
��
��![]() ��
��
��![]() ƽ��
ƽ��![]() ��
��
����![]() ��
��![]() ����
����![]() ��
��
������ȷ����________��(��������ȷ���۵���Ŷ�ѡ��)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ�е�����ͼ��K1��K2���������¶��壺��GΪͼ��K1������һ�㣬��HΪK2ͼ��������һ�㣬���G��H�����ľ�������Сֵ����������СֵΪͼ��K1��K2����������������ͼ1����֪��ABC��A��-1��-8����B��9,2����C��-1,2�����߳�Ϊ![]() ��������PQMN���Խ���NQƽ����x�������x���ϣ�
��������PQMN���Խ���NQƽ����x�������x���ϣ�
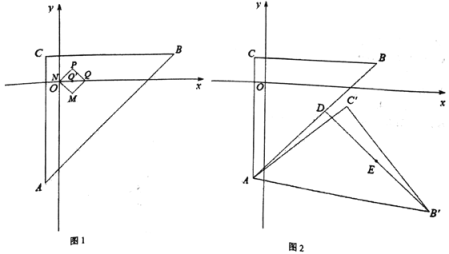
��1����գ�
��ԭ��O���߶�BC������������Ϊ ��
����ͼ1��������PQMN����ABC�ڣ�����O������Ϊ��m��0������������PQMN����ABC�ı߽������������Ϊ1����m��ȡֵ��ΧΪ ��
��2����֪������C��![]() ����-1��x��9����������C����ABC������������Ϊ1����a��ֵ��
����-1��x��9����������C����ABC������������Ϊ1����a��ֵ��
��3����ͼ2����֪��DΪ�߶�AB��һ�㣬��D��5��-2��������ABC�Ƶ�A˳ʱ����ת����0<����180��������ת�е���ABC��Ϊ��AB��C��������DB������EΪDB�����е㣬��������PQMN����O������Ϊ��5��-6����ֱ��д����������ת�����е�E�˶��γɵ�ͼ����������PQMN��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
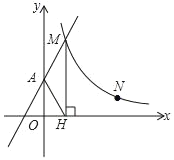
����Ŀ����ͼ��ֱ��y��2x+2��y�ύ��A�㣬�뷴��������y��![]() ��x��0����ͼ���ڵ�M����M��MH��x���ڵ�H����tan��AHO��2��
��x��0����ͼ���ڵ�M����M��MH��x���ڵ�H����tan��AHO��2��
��1����H������꼰k��ֵ��
��2����P��y���ϣ�ʹ��AMP����AMΪ���ĵ��������Σ���ֱ��д����������������P�����ꣻ
��3����N��a��1���Ƿ���������y��![]() ��x��0��ͼ���ϵĵ㣬��Q��m��0����x���ϵĶ��㣬����MNQ�����Ϊ3ʱ���������������������m��ֵ��
��x��0��ͼ���ϵĵ㣬��Q��m��0����x���ϵĶ��㣬����MNQ�����Ϊ3ʱ���������������������m��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com