
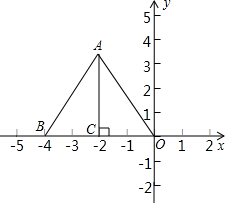 如图,把边长为4的等边三角形OAB置于平面直角坐标系中,点O与坐标原点重合,OB在x轴的负半轴上,点A在第二象限,AC⊥x轴于点C.
如图,把边长为4的等边三角形OAB置于平面直角坐标系中,点O与坐标原点重合,OB在x轴的负半轴上,点A在第二象限,AC⊥x轴于点C.分析 (1)由等边三角形的边长为4,求出OC,AC即可;
(2)先判断出以BD为底边,底角为30°的等腰三角形BDH的顶点在直线AB上或x轴,分两种情况先设出点H的坐标,用HB=HD建立方程即可;
(3)先设出点E的坐标,△COE的面积是以OC为底,点E的纵坐标的绝对值为高,建立方程求解即可.
解答 解:(1)∵△ABC是边长为4的等边三角形,
∴OC=BC=$\frac{1}{2}$0B=2,AC=2$\sqrt{3}$,
∵点A在第二象限,
∴A(-2,2$\sqrt{3}$),
(2)∵等边三角形的∠ABO的平分线交y轴于点D,
∴∠ABD=∠OBD=30°,
设直线BD的解析式为y=$\frac{\sqrt{3}}{3}$x+b,直线AB的解析式为y=$\sqrt{3}$x+m,
∵点B(-4,0)在直线BD和直线AB上,
∴b=$\frac{4\sqrt{3}}{3}$,m=4$\sqrt{3}$,
∴直线BD的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$,直线AB的解析式为y=$\sqrt{3}$x+4$\sqrt{3}$,
∴点D(0,$\frac{4\sqrt{3}}{3}$)
∵以BD为底边,底角为30°的等腰三角形BDH,
∴点H可能在直线AB上,也可能在x轴上,
①点H在x轴上时,设点H(n,0),
∴n-(-4)=$\sqrt{{n}^{2}+({\frac{4\sqrt{3}}{3})}^{2}}$,
∴n=-$\frac{4}{3}$,
∴H(-$\frac{4}{3}$,0),
②点H在直线AB上,设H(x,$\sqrt{3}$x+4$\sqrt{3}$),
∴AH=DH,
∴(x+4)2+($\sqrt{3}$x+4$\sqrt{3}$)2=x2+($\sqrt{3}$x+$\frac{8\sqrt{3}}{3}$)2,
∴x=-$\frac{8}{3}$,
∴H(-$\frac{8}{3}$,$\frac{4\sqrt{3}}{3}$),
∴点H(-$\frac{4}{3}$,0)或H(-$\frac{8}{3}$,$\frac{4\sqrt{3}}{3}$);
(3)设直线OA解析式为y=kx,
∵点A(-2,2$\sqrt{3}$)在直线OA上,
∴k=-$\sqrt{3}$,
∴直线OA解析式为y=-$\sqrt{3}$x,
设点E(a,-$\sqrt{3}$a)
∵OC=2,
∴S△COE=$\frac{1}{2}$×OC×|-$\sqrt{3}$a|=$\frac{1}{2}$×2×|$\sqrt{3}$a|=$\frac{\sqrt{3}}{4}$,
∴a1=$\frac{1}{4}$,a2=-$\frac{1}{4}$,
∴E1($\frac{1}{4}$,-$\frac{\sqrt{3}}{4}$),E2(-$\frac{1}{4}$,$\frac{\sqrt{3}}{4}$).
点评 此题是几何变换综合题,主要考查了等边三角形的性质,用待定系数法求直线解析式,平面内两点间的距离公式,解本题的关键是用待定系数法求直线解析式,根据点的特点设出点,建立方程是解本题的难点.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
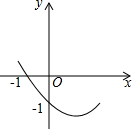 如图所示,已知二次函数y=ax2+bx+c的图象经过(-1,0)和(0,-1)两点,则化简代数式$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$=$\frac{2}{a}$.
如图所示,已知二次函数y=ax2+bx+c的图象经过(-1,0)和(0,-1)两点,则化简代数式$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$=$\frac{2}{a}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它的图象分布在第二、四象限 | B. | 它的图象与直线y=x无交点 | ||
| C. | 当x>0时,y的值随x的增大而增大 | D. | 当x<0时,y的值随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,O为直线AB上一点,且∠BOC=3∠AOC,OC平分∠AOD.
如图,O为直线AB上一点,且∠BOC=3∠AOC,OC平分∠AOD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当x=-1或x=2时,y=0 | D. | 当x>0时,y随x的增大而减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com