
����Ŀ��(1)��֪����A�ij������ֱ���2��1����ô�Ƿ������һ������B�������ܳ�������ֱ��Ǿ���A���ܳ��������2�������������⣬С��ͬѧ�ӡ�ͼ�Ρ��ĽǶȣ����ú���ͼ������˽��.С����֤�Ĺ��̿�ʼ�������ģ������x��y�ֱ��ʾ���εij��Ϳ�����ô����B����x��y��6��xy��4.���㰴��С������֤˼·��ɺ������֤����.(��ͼ��������˵����

(2)��֪����A�ij��Ϳ��ֱ���2��1����ô�Ƿ����һ������C�������ܳ�������ֱ��Ǿ���A���ܳ��������һ�룿С����Ϊ��������ǿ϶��ģ���ͬ��С���Ĺ۵���Ϊʲô��(ͬ��Ҫ��
���𰸡�(1)�𰸼�������(2)��ͬ�⣬���ɼ�����
�����������������(1)������ͬʱ����Ҫ��ĵ�(x��y)����һ�κ���y=-x+6��ͼ���뷴��������y=![]() ��ͼ���ڵ�һ�����ڽ�������꣬����н�����dz�����(2)���ֱ�һ�κ���y=-x+
��ͼ���ڵ�һ�����ڽ�������꣬����н�����dz�����(2)���ֱ�һ�κ���y=-x+![]() ��ͼ���뷴��������y=
��ͼ���뷴��������y=![]() ��ͼ��Ȼ�������ڵ�һ�����Ƿ��н���.
��ͼ��Ȼ�������ڵ�һ�����Ƿ��н���.
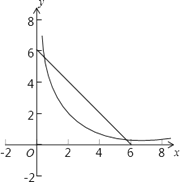
���������(1)���㣨x��y�����Կ���һ�κ���y=-x+6��ͼ���ڵ�һ�����ڵ�����꣬
�㣨x��y���ֿ��Կ�������������y=![]() ��ͼ���ڵ�һ�����ڵ�����꣬
��ͼ���ڵ�һ�����ڵ�����꣬
����������Ҫ��ĵ㣨x��y���Ϳ��Կ���һ�κ���y=-x+6��ͼ���뷴��������y=![]() ��ͼ���ڵ�һ�����ڽ�������꣮
��ͼ���ڵ�һ�����ڽ�������꣮
�ֱ���ͼ������ͼ������ͼ�пɿ����������Ľ�����ڣ�������Ҫ��ľ���B����.
(2)����ͬ��С���Ĺ۵㣮�����x��y�ֱ��ʾ���εij��Ϳ�����ô����C����x+y=![]() ��xy=1��
��xy=1��
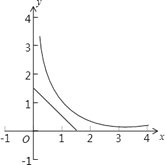
����Ҫ��ģ�x��y�����Կ���һ�κ���y=-x+![]() ��ͼ���뷴��������y=
��ͼ���뷴��������y=![]() ��ͼ���ڵ�һ�����ڽ�������꣮
��ͼ���ڵ�һ�����ڽ�������꣮
��ͼ������ͼ���ɿ����������Ľ��㲻���ڣ�������Ҫ��ľ���C�Dz����ڵģ����Բ�ͬ��С���Ĺ۵㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� ![]() ABCD�У�BC=7���ף�CD=5���ף���D=50�㣬BEƽ�֡�ABC�����н����д�����ǣ� ��
ABCD�У�BC=7���ף�CD=5���ף���D=50�㣬BEƽ�֡�ABC�����н����д�����ǣ� ��
A.��C=130��
B.��BED=130��
C.AE=5����
D.ED=2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C��D���ڡ�O�ϣ�FB���O�����ڵ�B��AB��CF���ڵ�G��OA��CF�ڵ�E��AC��BF��
��1����֤��FG=FB��
��2����tan��F=![]() ����O�İ뾶Ϊ4����CD�ij���
����O�İ뾶Ϊ4����CD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ѧ���Ժ������ȡ6��ѧ���ɼ����£�86��85��88��80��88��95��������������˵��������ǣ� ��
A. ������15 B. ������88 C. ��λ����86 D. ƽ������87
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD��32cm��AB��24cm����F�ӵ�B������B��C�����˶�����E�ӵ�D������D��A�����˶�����E�͵�F���ٶȶ�Ϊ3cm/s����E�˶�s���߶�EF�պñ�AC��ֱƽ�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬ֱ��l1��y=![]() x��ֱ��l2��y=��x+6���ڵ�A��l2��x�ύ��B����y�ύ�ڵ�C��
x��ֱ��l2��y=��x+6���ڵ�A��l2��x�ύ��B����y�ύ�ڵ�C��
��1������OAC�������
��2�����M��ֱ��l2�ϣ���ʹ����OAM���������OAC�����![]() �����M�����꣮
�����M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����PΪ��AOB��һ�㣬�ֱ�������P����OA��OB�ĶԳƵ�P1��P2 �� ����P1P2��OA��M����OB��N����P1P2=6�����PMN���ܳ�Ϊ �� 
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com