
 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(6,9).双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(6,9).双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.分析 (1)由点B的坐标及D为BC中点得出点D的坐标,据此可得k的值及反比例函数解析式,继而由点E横坐为6得出点E坐标;
(2)由点D、E坐标得出DB=3、BE=$\frac{9}{2}$,设点F(0,m),知CF=9-m、BC=6,再分△BCF∽△DBE、△BCF∽△EBD两种情况求得m的值,利用待定系数法可求得直线FB的解析式.
解答 解:(1)∵点B的坐标为(6,9),且四边形OABC是矩形,
∴OA=BC=6,OC=AB=9,
∵D为BC的中点,
∴点D坐标为(3,9),
将点D坐标代入y=$\frac{k}{x}$得:k=27,
∵OA=6,
∴在y=$\frac{27}{x}$中,当x=6时,y=$\frac{27}{6}$=$\frac{9}{2}$,
则点E坐标为(6,$\frac{9}{2}$),
故答案为:27、3、9、6、$\frac{9}{2}$;
(2)∵点D(3,9)、E(6,$\frac{9}{2}$),
∴DB=3,BE=$\frac{9}{2}$,
设点F(0,m),
则CF=9-m、BC=6,
①当△BCF∽△DBE时,$\frac{BC}{DB}$=$\frac{CF}{BE}$,
∴$\frac{6}{3}$=$\frac{9-m}{\frac{9}{2}}$,
解得:m=0,即点F(0,0),
设直线FB解析式为y=nx,
将点B(6,9)代入,得:n=$\frac{3}{2}$,
则直线BF解析式为y=$\frac{3}{2}$x;
②当△BCF∽△EBD时,$\frac{BC}{EB}$=$\frac{CF}{BD}$,
∴$\frac{6}{\frac{9}{2}}$=$\frac{9-m}{3}$,
解得:m=5,即点F(0,5),
设直线BF解析式为y=ax+b,
将点B(6,9)、F(0,5)代入,得:
$\left\{\begin{array}{l}{6a+b=9}\\{b=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=5}\end{array}\right.$,
则直线BF解析式为y=$\frac{2}{3}$x+5,
综上,直线BF解析式为y=$\frac{3}{2}$x或y=$\frac{2}{3}$x+5.
点评 此题属于反比例函数综合题,涉及的知识有:待定系数法求函数解析式,坐标与图形性质,相似三角形的性质,以及矩形的性质,熟练掌握待定系数法是解本题的关键.


科目:初中数学 来源: 题型:选择题

| A. | ①②③④ | B. | ④①③② | C. | ④②③① | D. | ④③②① |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
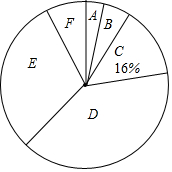 为了了解光明中学学生平均每周的体育锻炼时间,小敏在校内随机调查了50名同学,统计并绘制了频数分布表(如下表)和扇形统计图(如图).
为了了解光明中学学生平均每周的体育锻炼时间,小敏在校内随机调查了50名同学,统计并绘制了频数分布表(如下表)和扇形统计图(如图).| 组别 | 锻炼时间(h/周) | 频数 |
| A | 1.5≤t<3 | 1 |
| B | 3≤t<4.5 | 2 |
| C | 4.5≤t<6 | a |
| D | 6≤t<7.5 | 20 |
| E | 7.5≤t<9 | 15 |
| F | t≥9 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
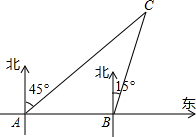 钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
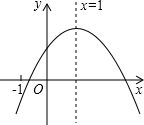 二次函数的图象如图所示,对称轴为x=1,给出下列结论:①abc<0;②b2>4ac;③4a+2b+c<0;④2a+b=0.其中正确的结论有( )
二次函数的图象如图所示,对称轴为x=1,给出下列结论:①abc<0;②b2>4ac;③4a+2b+c<0;④2a+b=0.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com