
【题目】已知直线y=2x﹣5与x轴和y轴分别交于点A和点B,抛物线y=﹣x2+bx+c的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.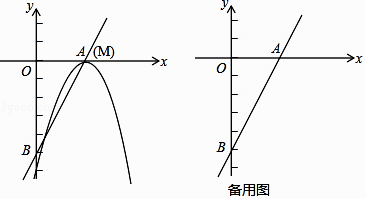
(1)如图,当点M与点A重合时,求抛物线的解析式;
(2)在(1)的条件下,求点N的坐标和线段MN的长;
(3)抛物线y=﹣x2+bx+c在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵直线y=2x﹣5与x轴和y轴分别交于点A和点B,
∴A( ![]() ,0),B(0,﹣5).
,0),B(0,﹣5).
当点M与点A重合时,∴M( ![]() ,0),
,0),
∴抛物线的解析式为y=﹣(x﹣ ![]() )2,即y=﹣x2+5x﹣
)2,即y=﹣x2+5x﹣ ![]()
(2)
解:N在直线y=2x﹣5上,设N(a,2a﹣5),又N在抛物线上,
∴2a﹣5=﹣a2+5a﹣ ![]() ,解得a1=
,解得a1= ![]() ,a2=
,a2= ![]() (舍去),
(舍去),
∴N( ![]() ,﹣4).
,﹣4).
过点N作NC⊥x轴,垂足为C,如图1
 ,
,
∵N( ![]() ,﹣4),
,﹣4),
∴C( ![]() ,0),
,0),
∴NC=4.MC=OM﹣OC= ![]() ﹣
﹣ ![]() =2,
=2,
∴MN= ![]() =
= ![]() =2
=2 ![]()
(3)
解:设M(m,2m﹣5),N(n,2n﹣5).
∵A( ![]() ,0),B(0﹣,5),
,0),B(0﹣,5),
∴OA= ![]() ,OB=5,则OB=2OA,AB=
,OB=5,则OB=2OA,AB= ![]() =
= ![]() ,
,
如图2
 ,
,
当∠MON=90°时,∵AB≠MN,且MN和AB边上的高相等,因此△OMN与△AOB不能全等,
∴△OMN与△AOB不相似,不满足题意;
当∠OMN=90°时, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得OM=
,解得OM= ![]() ,
,
则m2+(2m﹣5)2=( ![]() )2,解得m=2,∴M(2,﹣1);
)2,解得m=2,∴M(2,﹣1);
当∠ONM=90°时, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得ON=
,解得ON= ![]() ,则n2+(2n﹣5)2=(
,则n2+(2n﹣5)2=( ![]() )2,解得n=2,
)2,解得n=2,
∵OM2=ON2+MN2,即m2+(2m﹣5)2=5+(2 ![]() )2,解得m=4,则M点的坐标为(4,3),
)2,解得m=4,则M点的坐标为(4,3),
综上所述:M点的坐标为(2,﹣1)或(4,3)
【解析】(1)根据自变量与函数值的对应关系,可得A,B的值,根据顶点式,可得函数解析式;(2)根据函数图像上的点满足函数解析式,可得N点坐标,根据勾股定理,可得答案;(3)根据相似三角形的性质,可得关于m的方程,可得M点的坐标,要分类讨论,以防遗漏.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
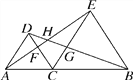
【题目】如图,在线段AB上取一点C(非中点),分别以AC、BC为边在AB的同侧作等边△ACD和等边△BCE,连接AE交CD于F,连接BD交CE于G,AE和BD交于点H,则下列结论:①AE=DB;②不另外添加线,图中全等三角形只有1对;③若连接FG,则△CFG是等边三角形;④若连接CH,则CH平分∠FHG.其中正确的是________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商店出售同样牌子和规格的羽毛球拍和羽毛球,每副球拍定价300元,每盒羽毛球定价40元,为庆祝五一节,两家商店开展促销活动如下:
甲商店:所有商品9折优惠;
乙商店:每买1副球拍赠送1盒羽毛球。
某校羽毛球队需要购买![]() 副球拍和
副球拍和![]() 盒羽毛球
盒羽毛球![]() .
.
(1)按上述的促销方式,该校羽毛球队在甲、乙两家商店各应花费多少元?试用含![]() 、
、![]() 的代数式表示;
的代数式表示;
(2)当![]() 时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?
时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?
(3)当![]() 、
、![]() 满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同?
满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节期间,某校倡议学生利用双休日“植树”劳动,为了解同学们劳动情况.学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回顾下列: 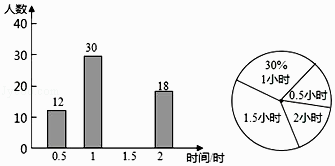
(1)通过计算,将条形图补充完整;
(2)扇形图形中“1.5小时”部分圆心角是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转,如图2,设旋转时间为t(0秒≤t≤90秒).
(1)用含t的代数式表示∠MOA的度数.
(2)在运动过程中,当∠AOB第二次达到60°时,求t的值.
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
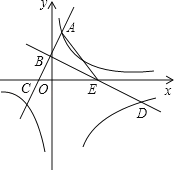
【题目】如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y=![]() 的图象的一个交点为A(1,m),过点B作AB的垂线BD,与反比例函数y=
的图象的一个交点为A(1,m),过点B作AB的垂线BD,与反比例函数y=![]() (x>0)的图象交于点D(n,﹣2).
(x>0)的图象交于点D(n,﹣2).
(1)k1和k2的值分别是多少?
(2)直线AB,BD分别交x轴于点C,E,若F是y轴上一点,且满足△BDF∽△ACE,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车油箱的容积为70升,小王把油箱注满油后准备驾驶汽车从县城到300千米外的省城接待客人,在接到客人后立即按原路返回,请回答下列问题:
(1)油箱注满油后,汽车能够行使的总路程y(单位:千米)与平均耗油量x(单位:升/千米)之间有怎样的函数关系?
(2)如果小王以平均每千米耗油0.1升的速度驾驶汽车到达省城,在返程时由于下雨,小王降低了车速,此时每行驶1千米的耗油量增加了一倍,如果小王一直以此速度行驶,邮箱里的油是否够回到县城?如果不够用,至少还需加多少油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF. 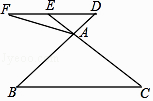
(1)如果 ![]() =
= ![]() ,DE=6,求边BC的长;
,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com