
【题目】如图,AD、BE分别是△ABC的中线,AD、BE相交于点F. 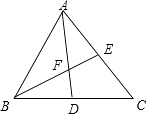
(1)△ABC与△ABD的面积有怎样的数量关系?为什么?
(2)△BDF与△AEF的面积有怎样的数量关系?为什么?
【答案】
(1)解:△ABC的面积是△ABD的面积的2倍.
理由:∵AD是△ABC的中线,
∴BD=CD,
又∵点A为△ABC的顶点,△ACD与△ABD同底等高,
∴△ACD的面积=△ABD的面积,
∴△ABC的面积是△ABD的面积的2倍

(2)解:△BDF与△AEF的面积相等.
理由:∵BE是△ABC的中线,
∴△ABC的面积是△ABE的面积的2倍,
又∵△ABC的面积是△ABD的面积的2倍,
∴△ABE的面积=△ABD的面积,
即△BDF的面积+△ABF的面积=△AEF的面积+△ABF的面积,
∴△BDF与△AEF的面积相等.
【解析】(1)根据三角形的中线将三角形分成面积相等的两部分进行判断;(2)根据三角形的中线将三角形分成面积相等的两部分,得出△ABE的面积=△ABD的面积,再根据△BDF的面积+△ABF的面积=△AEF的面积+△ABF的面积,得出结论即可.
【考点精析】本题主要考查了三角形的“三线”和三角形的面积的相关知识点,需要掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;三角形的面积=1/2×底×高才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
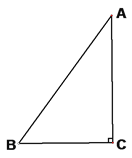
(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正值重庆一中85年校庆之际,学校计划利用校友慈善基金购买一些平板电脑和打印机.经市场调查,已知购买1台平板电脑比购买3台打印机多花费600元,购买2台平板电脑和3台打印机共需8400元.
(1)求购买1台平板电脑和1台打印机各需多少元?
(2)学校根据实际情况,决定购买平板电脑和打印机共100台,要求购买的总费用不超过168000元,且购买打印机的台数不低于购买平板电脑台数的2倍.请问最多能购买平板电脑多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD为菱形,连接BD,点E为菱形ABCD外任一点.
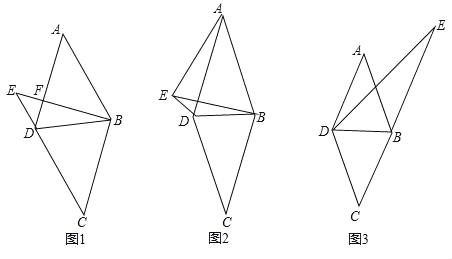
(1)如图(1),若∠A=45°,AB=![]() ,点E为过点B作AD边的垂线与CD边的延长线的交点,BE,AD交于点F,求DE的长.
,点E为过点B作AD边的垂线与CD边的延长线的交点,BE,AD交于点F,求DE的长.
(2)如图(2),若2∠AEB=180°﹣∠BED,∠ABE=60°,求证:BC=BE+DE
(3)如图(3),若点E在的CB延长线上时,连接DE,试猜想∠BED,∠ABD,∠CDE三个角之间的数量关系,直接写出结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+c>0,其中正确结论的个数为( ).

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简:
(1)(﹣1)2015﹣2﹣1+(π﹣3.14)0
(2)a3﹒a3+(﹣2a3)2﹣a8÷a2
(3)﹣5x(﹣x2+2x+1)﹣(2x﹣3)(5+x2)
(4)(x+3y﹣4z)(x﹣3y+4z)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列调查中,适宜采用普查的是( )
A.了解某校九(1)班学生视力情况B.调查2020年央视春晚的收视率
C.检测一批电灯泡的使用寿命D.了解我市中学生课余上网时间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com