练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．解方程组：$\left\{\begin{array}{l}{\frac{x}{7}=\frac{y}{10}=\frac{z}{5}}\\{x+2y+3z=84}\end{array}\right.$．

    分析 令第一个方程等于k，表示出x，y，z，代入第二个方程求出k的值，即可确定出方程组的解．

    解答 解：令$\frac{x}{7}$=$\frac{y}{10}$=$\frac{z}{5}$=k，可得x=7k，y=10k，z=5k，
    代入x+2y+3z=84中，得：7k+20k+15k=84，即k=2，
    则x=2k=14，y=10k=20，z=5k=10．
    则方程组的解为$\left\{\begin{array}{l}{x=14}\\{y=20}\\{z=10}\end{array}\right.$．

    点评 此题考查了解三元一次方程组，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．如图，抛物线y=ax2+bx与x轴交于点A，其顶点B在直线l：y=-x上，抛物线的对称轴与x轴交于点C（2，0）．
    （1）求抛物线的解析式；
    （2）抛物线上的点M（x0，y0）在x轴的下方，求当|y0|-|x0|取得最大值时点M的坐标；
    （3）在（2）的条件下，过点M且平行于y轴的直线交直线于点N，点P在抛物线上，点Q在直线BC上，问以N、B、P、Q为顶点能否构成平行四边形？若能，则求出点P的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．若max{S1，S2，…，Sn}表示实数S1，S2，…，Sn中的最大者．设A=（a1，a2，a3），B=$（\begin{array}{l}{b1}\\{b2}\\{b3}\end{array}）$，记A?B=max{a1b1，a2b2，a3b3}，设A=（x+1，$\frac{1}{2x}$，1），B=$（\begin{array}{l}{1}\\{4x^2-2x}\\{|x+1|}\end{array}）$，若A?B=x+1，则x的取值范围为-1≤x≤2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，A，B是直线l同侧的两点，作点A关于直线l的对称点A′，连结A′B．若点A，B到直线l的距离分别为2和3，则线段AB与A′B之间的数量关系是（　　）
    A．A′B2-AB2=13B．A′B2-AB2=24C．A′B2+AB2=25D．A′B2+AB2=26

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，是用相同长度的小棒摆成的一组有规律的图案，其中①需要4根小棒，图②需要10根小棒，…，按此规律摆下去，则第11个图案所需小棒的根数为（　　）
    A．70B．68C．64D．58

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．“奔跑吧，兄弟！”节目组，预设计一个新的游戏：“奔跑”路线需经A、B、C、D四地．如图，其中A、B、C三地在同一直线上，D地在A地北偏东30°方向、在C地北偏西45°方向．C地在A地北偏东75°方向．且BC=CD=20m．
    （1）证明三角形BCD是等边三角形；
    （2）从A地跑到D地的路程大约是多少？（最后结果保留整数，参考数据：sin15°=0.65，cos15°=0.97，tan15°=0.27，$\sqrt{2}$≈1.4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．正比例函数y=kx与反比例函数$y=\frac{m}{x}$图象的一个交点坐标是（3，2），则m-3k=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．某数学兴趣小组对线段上的动点问题进行探究，已知AB=8．
    问题思考：如图1，点P为线段AB上的一个动点，分别以AP、BP为边在同侧作正方形APDC与正方形PBFE．
    （1）在点P运动时，这两个正方形面积之和是定值吗？如果时求出；若不是，求出这两个正方形面积之和的最小值．
    （2）分别连接AD、DF、AF，AF交DP于点K，当点P运动时，在△APK、△ADK、△DFK中，是否存在两个面积始终相等的三角形？请说明理由．
    问题拓展：
    （3）如图2，以AB为边作正方形ABCD，动点P、Q在正方形ABCD的边上运动，且PQ=8．若点P从点A出发，沿A→B→C→D的线路，向D点运动，求点P从A到D的运动过程中，PQ的中点O所经过的路径的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

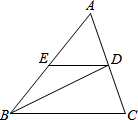    18．如图，在△ABC中，BD交AC于点D，DE交AB于点E，∠EBD=∠EDB，∠ABC：∠A：∠C=5：6：7，∠BDC=85°．
    （1）求∠BED的度数；
    （2）ED与BC有怎样的位置关系？为什么？

    查看答案和解析>>

    同步练习册答案