
【题目】如图,点P是射线BM上的一个动点(点P不与点B重合),∠AOB= 30°,∠ABM=60°.当∠OAP=______时,以点A、O、B中的任意两点和点P为顶点的三角形是等腰三角形.

【答案】75°或120°或90°
【解析】
先根据题意画出符合的情况,再根据等腰三角形的性质和三角形内角和定理求出即可.
分为以下5种情况:
①OA=OP,
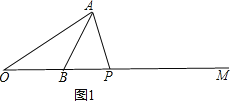
∵∠AOB=30°,OA=OP,
∴∠OAP=∠OPA=![]() ×(180°-30°)=75°;
×(180°-30°)=75°;
②OA=AP,
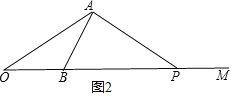
∵∠AOB=30°,OA=AP,
∴∠APO=∠AOB=30°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-30°=120°;
③AB=AP,
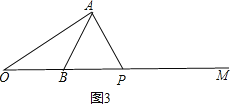
∵∠ABM=60°,AB=AP,
∴∠APO=∠ABM=60°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-60°=90°;
④AB=BP,
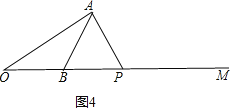
∵∠ABM=60°,AB=BP,
∴∠BAP=∠APO=![]() ×(180°-60°)=60°,
×(180°-60°)=60°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-60°=90°;
⑤AP=BP,
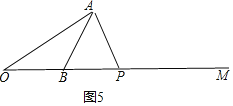
∵∠ABM=60°,AP=BP,
∴∠ABO=∠PAB=60°,
∴∠APO=180°-60°-60°=60°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-60°=90°;
所以当∠OAP=75°或120°或90°时,以A、O、B中的任意两点和P点为顶点的三角形是等腰三角形,
故答案为:75°或120°或90°.


科目:初中数学 来源: 题型:
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )

A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图中,每个正方形由边长为1的小正方形组成: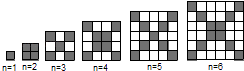
(1)观察图形,请填写下列表格:
正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
黑色小正方形个数 |
正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
黑色小正方形个数 |
(2)在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1 , 白色小正方形的个数为P2 , 问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )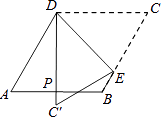
A.78°
B.75°
C.60°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
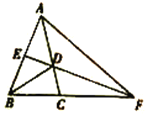
【题目】如图,在△ABC中.AB=AC.∠BAC=36°.BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.求证:(1)EF⊥AB; (2)△ACF为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生去福利院献爱心,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)向甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2400元,那么最多可购买多少个甲礼品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )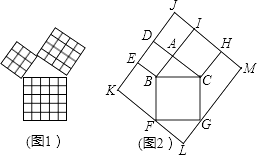
A.90
B.100
C.110
D.121
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com