
【题目】已知x≠1,(1+x)(1-x)=1-![]() ,(1-x)(1+x+
,(1-x)(1+x+![]() )=1-
)=1-![]() ,(1-x)(1+x+
,(1-x)(1+x+![]() +
+![]() )=1-
)=1-![]() .
.
(1)根据以上式子计算:
①(1-2)×(1+2+![]() +
+![]() +
+![]() +
+![]() ):②2+
):②2+![]() +
+![]() +…+
+…+![]() (n为正整数):
(n为正整数):
③(x-1)( ![]() +
+![]() +
+![]() +…+
+…+![]() +x+1).
+x+1).
(2)通过以上计算,请你进行下面的探索:
①(a-b)(a+b)=______________:②(a-b) (![]() +ab+
+ab+![]() )=_________________:
)=_________________:
③(a-b)( ![]() +
+![]() b+
b+![]() +
+![]() )=_____________.
)=_____________.
【答案】(1)①原式=-63;②原式=2n+1-2;③原式=x100-1;(2)①a2-b2;②a3-b3;③a4-b4
【解析】试题分析: (1)利用猜想的结论得到①(1-2)(1+2+22+23+24+25)=-63;
②先变形2+22+23+24+…+2n=2(1+2+22+23+24+…+2n-1)=-2(1-2)(1+2+22+23+24+…+2n-1),然后利用上述结论写出结果;
③先变形得到(x-1)(x99+x98+x97+…+x2+x+1)=-(1-x)(1+x+x2+…+x99),然后利用上述结论写出结果;
(2)(3)根据规律易得①(a-b)(a+b)=a2-b2;②(a-b)(a2+ab+b2)=a3-b3;③(a-b)(a3+a2b+ab2+b3)=a4-b4.
试题解析:
(1) ①(1-2)×(1+2+2![]() +2
+2![]() +2
+2![]() +2
+2![]() )
)
=1-26
=1-26
=1-64
=-63
②2+22+23+24+…+2n
=2(1+2+22+23+24+…+2n-1)
=-2(1-2)(1+2+22+23+24+…+2n-1)2(12n)
=2n+1-2
③(x-1)(x99+x98+x97+…+x2+x+1)
=-(1-x)(1+x+x2+…+x99)
=(1![]() )
)
=![]() 1
1
(2)
①(ab)(a+b)=ab;
②(ab)(a+ab+b)=ab;
③(ab)(a+ab+ab+b)=a4-b4.
点睛: 本题考查了整式的混合运算:先进行乘方运算,然后进行乘除运算,再进行加减运算;有括号先算括号.也考查了实数的运算.


科目:初中数学 来源: 题型:
【题目】【回归课本】我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
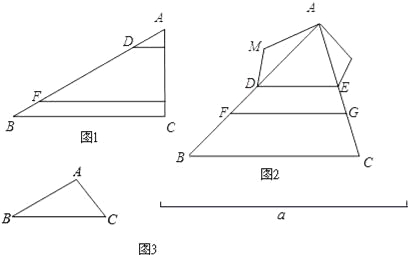
(1)如图1,在△ABC中,点D、F在AB上,E、G在AC上,DE∥FC∥BC.若AD=2,AE=1,DF=6,则EG= , ![]() = .
= .
(2)如图2,在△ABC 中,点D、F在AB上,E、G在AC上,且DE∥BC∥FG.以AD、DF、FB为边构造△ADM(即AM=BF,MD=DF);以AE、EG、GC为边构造△AEN(即AN=GC,NE=EG).
求证:∠M=∠N.
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题:
(3)如图3,已知△ABC和线段a,请用直尺与圆规作△A′B′C′.
满足:①△A′B′C′∽△ABC;②△A′B′C′的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地是一个降水丰富的地区,今年4月初,由于连续降雨导致该地某水库水位持续上涨,经观测水库1日—4日的水位变化情况,发现有这样规律, 1日,水库水位为![]() 米,此后日期每增加一天,水库水位就上涨
米,此后日期每增加一天,水库水位就上涨![]() 米。
米。
(1)请求出该水库水位![]() (米)与日期
(米)与日期![]() (日)之间的函数表达式;(注:4月1日,即
(日)之间的函数表达式;(注:4月1日,即![]() ,4月2日,即
,4月2日,即![]() ,…,以次类推)
,…,以次类推)
(2)请用求出的函数表达式预测该水库今年4月6日的水位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,你我同行”.今年合肥市区的增设的“小黄车”、“摩拜单车”等公共自行车
给市民出行带来了极大的方便.图①是某种公共自行车的实物图,图②是该种公共自行车的
车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,
座杆CE=15cm,且∠EAB=75°.求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°
≈0.26,tan75°≈3.73)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com