
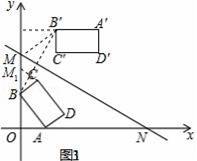
如图1,矩形ABCD的顶点A(6,0),B(0,8),AB=2BC,直线y=﹣
 x+m(m≥13)交坐标轴于M,N两点,将矩形ABCD沿直线y=﹣
x+m(m≥13)交坐标轴于M,N两点,将矩形ABCD沿直线y=﹣
 x+m(m≥13)翻折后得到矩形A′B′C′D′.
x+m(m≥13)翻折后得到矩形A′B′C′D′.
(1)求点C的坐标和tan∠OMN的值;
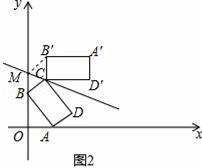
(2)如图2,直线y=﹣
 x+m过点C,求证:四边形BMB′C是菱形;
x+m过点C,求证:四边形BMB′C是菱形;
(3)如图1,在直线y=﹣
 x+m(m≥13)平移的过程中.
x+m(m≥13)平移的过程中.
①求证:B′C′∥y轴;
②若矩形A′B′C′D′的边与直线y=﹣x+43有交点,求m的取值范围.


【考点】一次函数综合题.
【分析】(1)首先利用勾股定理求得AB的长,然后证明△AOB∽△BEC,根据相似三角形的对应边的比相等求得BE的长,则OE长即可求得,从而求得C的坐标;
(2)利用待定系数法求得m的值,求得BM的长,根据四边相等的四边形是菱形即可证得;
(3)①连接BB′,根据(2)可得∠M1BB′=
 ∠MBC,然后根据对称性证明∠M1BB′=∠C′B′B,据此即可证得;
∠MBC,然后根据对称性证明∠M1BB′=∠C′B′B,据此即可证得;
②过B′作B′F⊥y轴于点F,设B′F=a,则BF=2a,设BM=B′M=b,则MF=2a﹣b,在直角△B′FM中利用勾股定理求得a和b的比值,MF和B′F即可利用m表示出来,B′和C′坐标即可求得,代入直线y=﹣x+43求得m的值,从而确定m的范围.
【解答】解:(1)∵A(6,0),B(0,8).
∴OA=6,OB=8,
∴AB=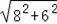
 =10,
=10,
∴BC=
 AB=5.
AB=5.
如图1,过C作CE⊥y轴于点E,
∴∠BOA=∠CEB=90°,
又∵∠BAO+∠ABO=∠EBC+∠ABO=90°,
∴∠BAO=∠BEC,
∴△AOB∽△BEC,
∴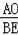
 =
=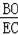
 =
=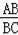
 =2,
=2,
∴BE=3,CE=4.
∴OE=BE﹣OB=11,
∴点C的坐标是(4,11).
当x=0时,OM=m,当y=0时,ON=2m,
∴tan∠OMN=2;
(2)如图2,由题意得:BM=BM′,BC=B′C.
∵直线y=﹣
 x+m过点C(4,11).
x+m过点C(4,11).
∴11=﹣2+m,
解得:m=13,
∴BM=13﹣8=5,
∴BM′=BM=BC=BC′=5,
∴四边形BMB′C是菱形;
(3)①如图3,连接BB′,由(2)已证∠M1BB′=
 ∠MBC,
∠MBC,
∵CM1∥MN,BB′⊥M1C,
∴∠MBB′=
 ∠MBC,
∠MBC,
由对称可得:∠C′B′B=∠CBB′,
∴∠M1BB′=∠C′B′B,
∴B′C′∥y轴.
②如图3,过B′作B′F⊥y轴于点F.
∵BB′⊥MN,
∴tan∠MBB′=
 ,
,
∴BF=2B′F,
设B′F=a,则BF=2a,设BM=B′M=b,则MF=2a﹣b,
在直角△B′FM中,a2+(2a﹣b)2=b2,
解得:a:b=4:5.
∴MF:B′F:B′M=3:4:5.
∵B′M=BM=m﹣8,
∴MF=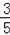
 (m﹣8),B′F=
(m﹣8),B′F=
 (m﹣8).
(m﹣8).
∴A′坐标是(
 ,
,
 ),C′(
),C′(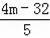
 ,
,
 ),
),
当点A′在直线y=﹣x++43上时,m=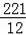
 ,
,
当点C′在直线y=﹣x+43上时,m=
 .
.
∴则b的取值范围是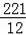
 ≤m≤
≤m≤
 .
.






 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一位同学做了一个斜面装置进行科学实验,△ABC是该装置左视图,∠ACB=90°,∠B=15°,为了加固斜面,在斜面AB的中点D处连结一条支撑杆CD,量得CD=6.
(1)求斜坡AB长和∠ADC的度数;
(2)该同学想用彩纸实验装置中的△ABC的表面,请你计算△ABC的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
我校2016级2198名考生在2016年中考体育考试中取得了优异成绩,为了考察他们的中考体育成绩,从中抽取了550名考生的中考体育成绩进行统计,下列说法正确的是( ).
A.本次调查属于普查
B.每名考生的中考体育成绩是个体
C.550名考生是总体的一个样本
D.2198名考生是总体
查看答案和解析>>
科目:初中数学 来源:2016届上海市奉贤区九年级上学期期末调研考试数学试卷(解析版) 题型:解答题
如图,在 O中,AB为直径,点B 为
O中,AB为直径,点B 为 的中点,直径AB交弦CD于E ,CD =2
的中点,直径AB交弦CD于E ,CD =2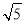 ,AE=5.
,AE=5.

(1)求 O半径r 的值;
O半径r 的值;
(2)点F 在直径AB上,联结CF ,当∠FCD =∠DOB时,求 AF 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2015-2016学年江苏省八年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系中,一个点从A(a1,a2)出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此一直运动下去,则a2015+a2016的值为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com