
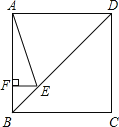
【题目】如图,正方形ABCD的边长为4,点E对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长为( )
A. 1B. 4-![]() C.
C. ![]() D.
D. ![]() -4
-4
【答案】B
【解析】
在AF上取FG=EF,连接GE,可得△EFG是等腰直角三角形,根据等腰直角三角形的性质可得EG=![]() EF,∠EGF=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAE+∠AEG=∠EGF,然后求出∠BAE=∠AEG=22.5°,根据等角对等边可得AG=EG,再根据正方形的对角线平分一组对角求出∠ABD=45°,然后求出△BEF是等腰直角三角形,根据等腰直角三角形的性质可得BF=EF,设EF=x,最后根据AB=AG+FG+BF列方程求解即可.
EF,∠EGF=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAE+∠AEG=∠EGF,然后求出∠BAE=∠AEG=22.5°,根据等角对等边可得AG=EG,再根据正方形的对角线平分一组对角求出∠ABD=45°,然后求出△BEF是等腰直角三角形,根据等腰直角三角形的性质可得BF=EF,设EF=x,最后根据AB=AG+FG+BF列方程求解即可.
解:如图,在AF上取FG=EF,连接GE,
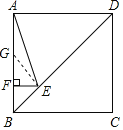
∵EF⊥AB,
∴△EFG是等腰直角三角形,
∴EG=![]() EF,∠EGF=45°,
EF,∠EGF=45°,
由三角形的外角性质得,∠BAE+∠AEG=∠EGF,
∵∠BAE=22.5°,∠EGF=45°,
∴∠BAE=∠AEG=22.5°,
∴AG=EG,
在正方形ABCD中,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴BF=EF,
设EF=x,∵AB=AG+FG+BF,
∴4=![]() x+x+x,
x+x+x,
解得x=2(2-![]() )=4-2
)=4-2![]() .
.
故选:B.


科目:初中数学 来源: 题型:
【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:

(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;
又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
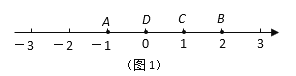
知识运用:如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.
(1)数_______________________ 所表示的点是(M,N)的好点;
(2)数________________________ 所表示的点是(N,M)的好点;

(温馨提示:注意考虑M,N的左侧、右侧,不要漏掉答案)
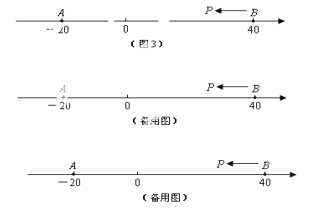
(3)如图(3)A,B为数轴上的两点,点A所表示的数为-20,点B表示的数为 40,现有一只电子蚂蚁P从点B出发,以2单位每秒的速度一直向左运动,
①当t为何值时,P是(A,B)的好点?
②当t为何值时,P是(B,A)的好点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化,源远流长,在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:
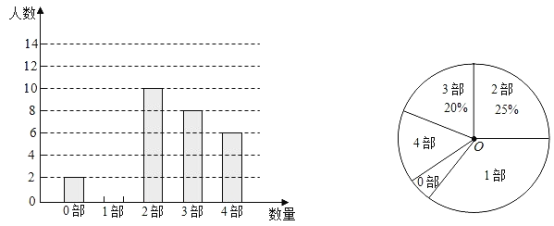
(1)请补全条形分布直方图,本次调查一共抽取了 名学生;
(2)扇形统计图中“1部”所在扇形的圆心角为 度;
(3)若该中学有1000名学生,请估计至少阅读3部四大古典名著的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=120°,点E,F分别在边AB,BC上,将菱形沿EF折叠,点B恰好落在AD边上的点G处,且EG⊥AC,若CD=8,则FG的长为( )
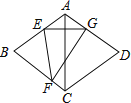
A. 6B. ![]() C. 8D.
C. 8D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,把超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:克) | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)若每袋食品的标准质量为450克,则抽样检测的20袋食品的总质量是多少克?
(2)若该种食品的合格标准为450±5克,求该种食品抽样检测的合格率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探索发现】
如图①,是一张直角三角形纸片,∠B=90°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
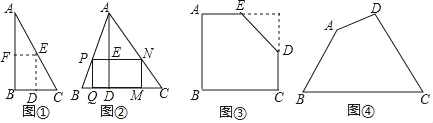
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
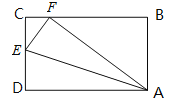
【题目】如图,四边形ABCD是矩形纸片,AD=10,CD=8,在CD边上取一点E,将纸片沿AE折叠,使点D落在BC边上的F处.
(1)AF的长=_____.
(2)BF的长=______.
(3)CF的长=_____.
(4)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程![]() ,给出下列结论:
,给出下列结论:
①存在实数a,使得x,y的值互为相反数;
②当a=2时,方程组的解也是方程3x+y=4+a的解;
③x,y都为自然数的解有3对.
其中正确的是( )
A.①②B.②③C.①③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com