
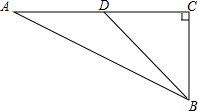
 在Rt△ABC中,∠C=90°,AB=10$\sqrt{3}$,∠A=30°,求BD+$\frac{1}{2}$AD和2BD+$\sqrt{2}$AD的最小值.
在Rt△ABC中,∠C=90°,AB=10$\sqrt{3}$,∠A=30°,求BD+$\frac{1}{2}$AD和2BD+$\sqrt{2}$AD的最小值. 分析 在AC的上方作∠EAC=30°,延长BC交AE于点E,过点B作BF⊥AE于点F交AC于点D,此时BD+$\frac{1}{2}$AD最小,根据边角关系可得出△ABE为等边三角形,由此即可得出BD+$\frac{1}{2}$AD的最小值;在AC的上方作∠MAC=45°,延长BC交AM于点M,过点B作BN⊥AM于点N交AC于点D,此时2BD+$\sqrt{2}$AD最小,根据边角关系可得出△BMN为等腰直角三角形,利用特殊角的三角形函数值找出BC和AC的长度,进而可得出BF的长度,由此即可得出2BD+$\sqrt{2}$AD的最小值.
解答 解:在AC的上方作∠EAC=30°,延长BC交AE于点E,过点B作BF⊥AE于点F交AC于点D,此时BD+$\frac{1}{2}$AD最小,如图1所示.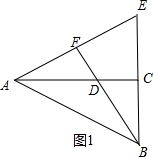
∵∠BAC=30°,∠EAC=30°,
∴∠BAE=60°.
∵∠ACB=90°,
∴AC⊥BE.
∵AC为∠BAE的角平分线,
∴△ABE为等边三角形.
∵AB=10$\sqrt{3}$,
∴BE=BD+DF=BD+$\frac{1}{2}$AD=$\frac{\sqrt{3}}{2}$AB=15.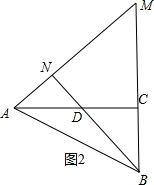
∴BD+$\frac{1}{2}$AD的最小值为15.
在AC的上方作∠MAC=45°,延长BC交AM于点M,过点B作BN⊥AM于点N交AC于点D,此时2BD+$\sqrt{2}$AD最小,如图2所示.
∵∠MAC=45°,∠ACB=90°,
∴△ACM为等腰直角三角形,∠AMC=45°.
在Rt△ABC中,AB=10$\sqrt{3}$,∠BAC=30°,∠ACB=90°,
∴BC=AB•sin∠BAC=5$\sqrt{3}$,AC=AB•cos∠BAC=15.
∴MC=AC=15.
∵BN⊥AM,
∴△BMN为等腰直角三角形,
∵BM=BC+MC=5$\sqrt{3}$+15,
∴BN=BD+DN=BD+$\frac{\sqrt{2}}{2}$AD=$\frac{\sqrt{2}}{2}$BM=$\frac{5\sqrt{6}+15\sqrt{2}}{2}$,
∴2BD+$\sqrt{2}$AD的最小值为5$\sqrt{6}$+15$\sqrt{2}$.
点评 本题考查了特殊角的三角函数值、等边三角形的判定与性质以及等腰直角三角形的判定与性质,解题的关键是找出点D的位置.本题属于中档题,难度不大,解决该题型题目时,根据题意画出图形,利用数形结合解决问题是关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
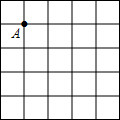 如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.
如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
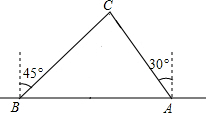 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我国两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域,如图,在B处测得C在东北方向上,在A处测得C在北偏西30°的方向上.
为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我国两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域,如图,在B处测得C在东北方向上,在A处测得C在北偏西30°的方向上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
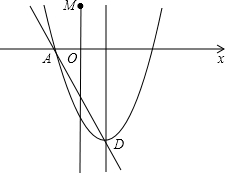 如图所示.抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点.
如图所示.抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
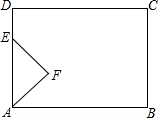 如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).
如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
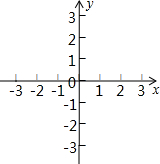 已知二次函数y=x2+bx+3的图象经过点(3,0).
已知二次函数y=x2+bx+3的图象经过点(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
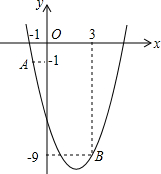 如图,已知抛物线y=ax2-4x+c的图象经过点A和点B.
如图,已知抛物线y=ax2-4x+c的图象经过点A和点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com