
【题目】甲,乙,丙三人各有邮票若干枚,要求互相赠送.先由甲送给乙,丙,所给的枚数等于乙,丙原来各有的邮票数;然后依同样的游戏规则再由乙送给甲,丙现有的邮票数,最后由丙送给甲,乙现有的邮票数.互相送完后,每人恰好各有64枚.你能知道他们原来各有邮票多少枚吗?说出你的思考过程.
【答案】解:设甲原有邮票x枚,乙原有邮票y枚,丙原有邮票z枚.
甲 | 乙 | 丙 | |
原有 | x | y | z |
第一次送后 | x﹣y﹣z | 2y | 2z |
第二次送后 | 2(x﹣y﹣z) | 2y﹣(x﹣y﹣z)﹣2z | 4z |
第三次送后 | 4(x﹣y﹣z) | 2[2y﹣(x﹣y﹣z)﹣2z] | 4z﹣2(x﹣y﹣z)﹣[2y﹣(x﹣y﹣z)﹣2z] |
根据第三次赠送后列方程组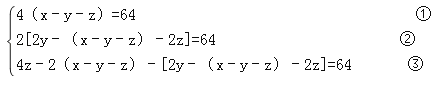 ,
,
即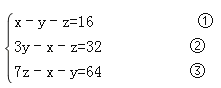 ,
,
③﹣②得 2z﹣y=8 ④,
②+①得 y﹣z=24 ⑤,
④+⑤得 z=32,
将z代入⑤得 y=56,
将y、z代入①得 x=104,
答:甲原有邮票104枚,乙原有邮票56枚,丙原有邮票32枚.
【解析】假设甲原有邮票x枚,乙原有邮票y枚,丙原有邮票z枚.根据题目说明列出三次赠送的过程如下表
甲 | 乙 | 丙 | |
原有 | x | y | z |
第一次送后 | x﹣y﹣z | 2y | 2z |
第二次送后 | 2(x﹣y﹣z) | 2y﹣(x﹣y﹣z)﹣2z | 4z |
第三次送后 | 4(x﹣y﹣z) | 2[2y﹣(x﹣y﹣z)﹣2z] | 4z﹣2(x﹣y﹣z)﹣[2y﹣(x﹣y﹣z)﹣2z] |
根据第三次赠送后的结果列出方程组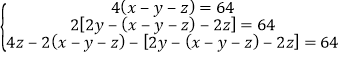
先化简,最后代入消元法或加减消元法求出方程组的解即可.
【考点精析】通过灵活运用解三元一次方程组,掌握通过“代入”或“加减”消元,把“三元”化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某服装点用6000购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
类型 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)求这两种服装各购进的件数;
(2)如果A种服装按标价的8折出售,B种服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,求黄花一共用了多少朵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组数据为1,5,3,4,5,6,这组数据的极差、众数、中位数分别为( )
A. 4,4,5 B. 5,5,4.5 C. 5,5,4 D. 5,3,2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点C,交AB的延长线于点E,连接CD、CE.

(1)求证:△ACD∽△AEC;
(2)当![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4![]() ,求△ACE的面积.
,求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道a+b=0时,a3+b3=0也成立,若将a看成a3的立方根,b看成b3的立方根,我们能否得出这样的结论:若两个数的立方根互为相反数,则这两个数也互为相反数.
(1)试举一个例子来判断上述猜测结论是否成立;
(2)若![]() 与
与![]() 互为相反数,求
互为相反数,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com