
【题目】如图,正方形ABCD的边长是2个单位,一只乌龟从A点出发以2个单位/秒的速度顺时针绕正方形运动,另有一只兔子也从A点出发以6个单位/秒的速度逆时针绕正方形运动,则第2018次相遇在( )

A. 点A B. 点B C. 点C D. 点D
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=kx+b图象与x轴相交于点A,与反比例函数 ![]() 的图象相交于B(﹣1,5)、C(
的图象相交于B(﹣1,5)、C( ![]() ,d)两点.点P(m,n)是一次函数y1=kx+b的图象上的动点.
,d)两点.点P(m,n)是一次函数y1=kx+b的图象上的动点.
(1)求k、b的值;
(2)设﹣1<m< ![]() ,过点P作x轴的平行线与函数
,过点P作x轴的平行线与函数 ![]() 的图象相交于点D.试问△PAD的面积是否存在最大值?若存在,请求出面积的最大值及此时点P的坐标;若不存在,请说明理由;
的图象相交于点D.试问△PAD的面积是否存在最大值?若存在,请求出面积的最大值及此时点P的坐标;若不存在,请说明理由;
(3)设m=1﹣a,如果在两个实数m与n之间(不包括m和n)有且只有一个整数,求实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点A(0,﹣4)的抛物线y= ![]() x2+bx+c与x轴相交于B(﹣2,0),C两点,O为坐标原点.
x2+bx+c与x轴相交于B(﹣2,0),C两点,O为坐标原点.
(1)求抛物线的解析式;
(2)将抛物线y= ![]() x2+bx+c向上平移
x2+bx+c向上平移 ![]() 个单位长度,再向左平移m(m>0)个单位长度得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
个单位长度,再向左平移m(m>0)个单位长度得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
(3)设点M在y轴上,∠OMB+∠OAB=∠ACB,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选出2名同学打第一场比赛,求下列事件的概率:
(1)已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学;
(2)随机选取2名同学,其中有乙同学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人分别从A(1, ![]() )、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
)、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点. 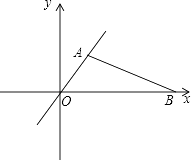
(1)请说明甲、乙两人到达O点前,MN与AB不可能平行;
(2)当t为何值时,△OMN∽△OBA;
(3)甲、乙两人之间的距离为MN的长,设s=MN2 , 求s与t之间的函数关系式,并求甲、乙两人之间距离的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑩的直角顶点的坐标为 . 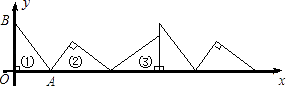
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com