
【题目】如图①,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC(如图②),且∠B=30°,∠C=100°,则下列说法正确的是( )
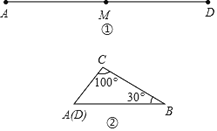
A. 点M在AB上B. 点M在BC上,且距点B较近,距点C较远
C. 点M在BC的中点处D. 点M在BC上,且距点C较近,距点B较远
科目:初中数学 来源: 题型:
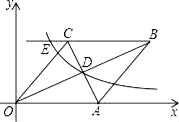
【题目】如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=![]() (x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
(x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
①双曲线的解析式为y=![]() (x>0);
(x>0);
②E点的坐标是(5,8);
③sin∠COA=![]() ;
;
④AC+OB=12![]() .
.
其中正确的结论有 (填上序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与抛物线
与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
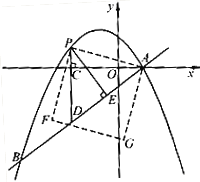
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作如图所示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,求出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
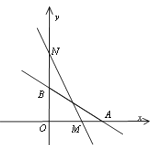
【题目】如图,直线L:![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,在y轴上有一点
两点,在y轴上有一点![]() ,动点M从A点出发以每秒1个单位的速度沿射线AO匀速运动.
,动点M从A点出发以每秒1个单位的速度沿射线AO匀速运动.
(1)点A的坐标: ;点B的坐标: ;
(2)求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() ,求出此时点M的坐标;
,求出此时点M的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班所有学生参加2010年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:

(1)九年级(1)班参加体育测试的学生有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级B部分所占的百分比是 ,等级C对应的圆心角的度数为 ;
(4)若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
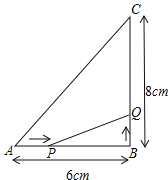
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,
(1)如果P、Q同时出发,几秒后,可使△PBQ的面积为8平方厘米?
(2)线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量一个圆铁环的半径,某同学用了如下方法,将铁环平放在水平桌面上,用有一个角为30°的直角三角板和刻度尺按如图所示的方法得到相关数据,进而求出铁环半径,若测得PA=5cm,则铁环的半径是_____cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com