
【题目】(1)如图1,△ABC中,D是BC边上一点,则△ABD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为![]() (△ABD、△ADC的面积分别用记号
(△ABD、△ADC的面积分别用记号![]() 、
、![]() 表示).现有
表示).现有![]() ,则
,则![]() .
.
(2)如图2,△ABC中,E、F分别是BC、AC边上一点,且有![]() ,
, ![]() ,AE与BF相交于点G.现作EH∥BF交AC于点H.依次求
,AE与BF相交于点G.现作EH∥BF交AC于点H.依次求![]() 、
、![]() 、
、![]() 的值.
的值.
(3)如图3,△ABC中,点P在边AB上,点M、N在边AC上,且有![]() ,
, ![]() ,
,
BM、BN与CP分别相交于点R、Q.现已知△ABC的面积为1,求△BRQ的面积.

科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M. 
(1)若∠B=70°,则∠NMA的度数是 .
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
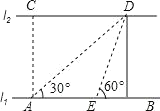
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,C,对称轴是x=﹣3,请解答下列问题:
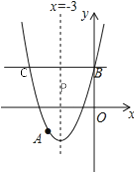
(1)求抛物线的解析式.
(2)求点B的坐标;
(3)过点B作与x轴平行的直线交抛物线交点C,在抛物线的对称轴上的确存在一点P,使PA+PC的值最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场把一个双肩背的书包按进价提高60%标价,然后再按8折(标价的80%)出售,这样商场每卖出一个书包就可赢利14元.这种书包的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】莫菲、隆迪、紫惠和曲代4人一起去火锅店吃火锅,4人在如图所示的四人桌前就座,其中莫菲和紫惠坐在餐桌的同侧,
(1)请用适当的方法表示出所有的不同就座方案.
(2)请问隆迪恰好坐在靠近过道一侧的概率是多少?
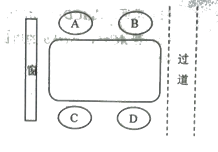
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中,正确的是( )
①三个点确定一个圆;②同弧或等弧所对的圆周角相等;③平分弦的直径垂直于弦,并且平分弦所对的弧;④圆内接平行四边形一定是矩形。
A.①②B.②③C.②④D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见下表:
A型销售数量(台) | B型销售数量(台) | 总利润(元) |
5 | 10 | 2 000 |
10 | 5 | 2 500 |
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300 m3/小时,B型空气净化器的净化能力为200 m3/小时.某长方体室内活动场地的总面积为200 m2,室内墙高3 m.该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,如不考虑空气对流等因素,至少要购买A型空气净化器多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com