练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知二次函数的图象与轴分别交于A(1,0),B(3,,0)两点，与轴交于点C.

    （1）求此二次函数解析式；

    （2）点D为抛物线的顶点，试判断的形状，并说明理由.

    【答案】（1）；（2）为直角三角形，理由详见解析.

    【解析】

    （1）利用待定系数法进行求解即可得；

    （2）先求出抛物线顶点坐标，然后利用勾股定理分别求出CD、BC、BC的长，然后再利用勾股定理逆定理进行求解即可得△BCD为直角三角形.

    （1）将A、B两点坐标分别代入函数，得

    ，解得，

    所以，二次函数解析式为y=x2-4x+3；

    （2）△BCD为直角三角形，理由如下：

    ∵y=x2-4x+3=(x-2)2-1，

    ∴抛物线顶点坐标D（2，-1），

    ，

    ，

    ，，

    ，

    ∴，

    ∴△BCD为直角三角形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知，点A(t,1)是平面直角坐标系中第一象限的点，点B,C分别是y轴负半轴和x轴正半轴上的点，连接AB,AC,BC.

    （1）如图1,若OB=1,OC =,且A,B,C在同一条直线上，求t的值；

    （2）如图 2,当 t =1，∠ACO +∠ACB = 180°时，求 BC + OC -OB 的值；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，点G在对角线BD上（不与点B，D重合），GE⊥DC于点E，GF⊥BC于点F，连结AG．

    （1）写出线段AG，GE，GF长度之间的数量关系，并说明理由；

    （2）若正方形ABCD的边长为1，∠AGF=105°，求线段BG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，AD是△ABC的中线，AE⊥AB，AF⊥AC，且AE=AB，AF=AC，AD=3，AB=4．

    （1）求AC长度的取值范围；

    （2）求EF的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠BAC＝90°，分别以AC，BC为边长，在三角形外作正方形ACFG和正方形BCED．若AC＝4，AB＝6，则EF＝______．

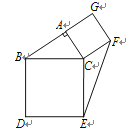
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC是边长为5cm的等边三角形，点P，Q分别从顶点A，B同时出发，沿线段AB，BC运动，且它们的速度都为1cm/s．当点P到达点B时，P，Q两点停止运动，设点P的运动时间为t（s）．

    （1）当t为何值时，△PBQ是直角三角形？

    （2）连接AQ、CP，相交于点M，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中华文明，源远流长；中华汉字，寓意深广，为传承中华优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写大赛”为了解本次大赛的成绩，校团委随机抽取了其中若干名学生的成绩作为样本进行统计，制成如下不完整的统计图表：

    成绩分

    频数人

    频率

    10

    　

    30

    　

    40

    n

    　

    m

    　

    50

    a

    1

    请根据所给信息，解答下列问题：

    ______，______，______；

    补全频数直方图；

    这若干名学生成绩的中位数会落在______分数段；

    若成绩在90分以上包括90分的为“优”等，请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下面的证明：如图，AB∥CD∥GH，EG平分∠BEF，FG平分∠EFD，

    求证：∠EGF＝90°．

    证明：∵AB∥GH（已知），

    ∴∠1＝∠3（　 　），

    又∵CD∥GH（已知），

    ∴　 　（两直线平行，内错角相等）

    ∵AB∥CD（已知），

    ∴∠BEF+　 　＝180°（两直线平行，同旁内角互补）

    ∵EG平分∠BEF（已知），

    ∴∠1＝ 　 　（角平分线定义），

    又∵FG平分∠EFD（已知），

    ∴∠2＝∠EFD（　 　），

    ∴∠1+∠2＝（　 　+∠EFD）

    ∴∠l+∠2＝90°，

    ∴∠3+∠4＝90°（等量代换），

    即∠EGF＝90°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中是真命题的是（ ）

    A. 有两边和其中一边的对角对应相等的两个三角形全等

    B. 两条平行直线被第三条直线所截，则一组同旁内角的平分线互相垂直

    C. 三角形的一个外角等于两个内角的和

    D. 等边三角形既是中心对称图形，又是轴对称图形

    查看答案和解析>>

    同步练习册答案