
【题目】在四边形ABCD中,E、F分别是边BC、CD的中点,连接AE,AF.
(1)如图1,若四边形ABCD的面积为5,则四边形AECF的面积为____________;
(2)如图2,延长AE至G,使EG=AE,延长AF至H,使FH=AF,连接BG、GH、HD、DB.
求证:四边形BGHD是平行四边形;
(3)如图3,对角线 AC、BD相交于点M, AE与BD交于点P, AF与BD交于点N. 直接写出BP、PM、MN、ND的数量关系.

【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]() .
.
【解析】
(1)连接AC,根据三角形中线把三角形分成两个面积相等的三角形进行解答即可得;
(2)连接EF,根据三角形中位线定理可得到BD与GH平行且相等,由此即可得证;
(3)如图,延长PE至点Q,使EQ=EP,连接CQ,延长NF至点O,使OF=NG,连接CO,通过证明△BPE≌△CQE可得BP=CQ,BP//CQ,同理:CO=ND,CO//ND,从而可得Q、C、O三点共线,继而通过证明△APM∽△AQC,可得PM:CQ=AM:AC,同理:MN:CO=AM:AC,即可得答案.
(1)如图,连接AC,则有S△ABC+S△ACD= S四边形ABCD=5,
∵E、F分别为BC、CD中点,
∴S△AEC=![]() S△ABC,S△AFC=
S△ABC,S△AFC=![]() S△ADC,
S△ADC,
∴S四边形AECF=S△AEC+S△AFC=![]() S△ABC+
S△ABC+![]() S△ADC=
S△ADC=![]() S四边形ABCD=
S四边形ABCD=![]() ,
,
故答案为:![]() ;
;

(2)如图,连接EF,
∵E、F分别是BC,CD的中点,
∴EF∥BD,EF=![]() BD.,
BD.,
∵EG=AE,FH=AF,
∴EF∥GH,EF=![]() GH.,
GH.,
∴BD∥GH,BD=GH.,
∴四边形BGHD是平行四边形;

(3)如图,延长PE至点Q,使EQ=EP,连接CQ,
延长NF至点O,使OF=NG,连接CO,
在△BPE和△CQE中
 ,
,
∴△BPE≌△CQE(SAS),
∴BP=CQ,∠PBE=∠QCE,
∴BP//CQ,
同理:CO=ND,CO//ND,
∴Q、C、O三点共线,
∴BD//OQ,
∴△APM∽△AQC,
∴PM:CQ=AM:AC,
同理:MN:CO=AM:AC,
∴![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形硬纸片ABCD中,![]() ,
,![]() ,
,![]() ,沿着对角线BD将平行四边形剪开成两个三角形,固定
,沿着对角线BD将平行四边形剪开成两个三角形,固定![]() 不动,将
不动,将![]() 沿射线BD方向以每秒1个单位的速度匀速运动
沿射线BD方向以每秒1个单位的速度匀速运动![]() 运动后
运动后![]() 记为
记为![]() 连接
连接![]() 和
和![]() .
.
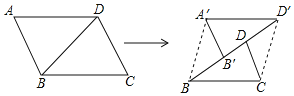
![]() 小明认为在运动过程中,始终有
小明认为在运动过程中,始终有![]() ,你同意吗?请说明理由.
,你同意吗?请说明理由.
![]() 保持上述条件不变,当
保持上述条件不变,当![]() 运动______秒时,四边形
运动______秒时,四边形![]() 为菱形.
为菱形.
![]() 保持上述条件不变,当
保持上述条件不变,当![]() 运动______秒时,四边形
运动______秒时,四边形![]() 为矩形.
为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定向越野作为一种新兴的运动项目,深受人们的喜爱. 这种定向运动是利用地图和指北针到访地图上所指示的各个点标,以最短时间按序到达所有点标者为胜. 下面是我区某校进行定向越野活动中,中年男子组的成绩(单位:分:秒).
9:01 14:45 9:46 19:22 11:20 18:47 11:40 12:32 11:52 13:45
22:27 15:00 17:30 13:22 18:34 10:45 19:24 16:26 21:33 15:31
19:50 14:27 15:55 16:07 20:43 12:13 21:41 14:57 11:39 12:45
12:57 15:31 13:20 14:50 14:57 9:41 12:13 14:27 12:25 12:38
例如,用时最少的赵老师的成绩为9:01,表示赵老师的成绩为9分1秒.

以下是根据某校进行定向越野活动中,中年男子组的成绩中的数据,绘制的统计图表的一部分.
某校中年男子定向越野成绩分段统计表
分组/分 | 频数 | 频率 |
9≤x<11 | 4 | 0.1 |
11≤x<13 | b | 0.275 |
13≤x<15 | 9 | 0.225 |
15≤x<17 | 6 | d |
17≤x<19 | 3 | 0.075 |
19≤x<21 | 4 | 0.1 |
21≤x<23 | 3 | 0.075 |
合计 | a | c |
(1)这组数据的极差是____________;
(2)上表中的a =____________ ,b =____________ , c =____________, d =____________;
(3)补全频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l分别交x轴、y轴于A、B两点,AB=5,OA:OB =3:4.
(1)求直线l的表达式;
(2)点P是![]() 轴上的点,点Q是第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.
轴上的点,点Q是第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC;OE平分∠BOC.
(1)图中∠BOD的邻补角为______;∠AOE的邻补角为______.
(2)如果∠COD=25°,那么∠COE=______;如果∠COD=60°,那么∠COE=______;
(3)试猜想∠COD与∠COE具有怎样的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠COE=90°,OF平分∠AOE.
(1)若∠COF=40°,求∠BOE的度数.
(2)若∠COF=α(0°<α<90°),则∠BOE=______(用含α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,点E,F分别在边BC,AD上,且AF=CE.

(Ⅰ)如图①,求证四边形AECF是平行四边形;
(Ⅱ)如图②,若∠BAC=90°,且四边形AECF是边长为6的菱形,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,中原福塔(河南广播电视塔)是世界第﹣高钢塔.小明所在的课外活动小组在距地面268米高的室外观光层的点D处,测得地面上点B的俯角α为45°,点D到AO的距离DG为10米;从地面上的点B沿BO方向走50米到达点C处,测得塔尖A的仰角β为60°.请你根据以上数据计算塔高AO,并求出计算结果与实际塔高388米之间的误差.(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414.结果精确到0.1米)
≈1.414.结果精确到0.1米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com