
 如图,用边长为1的正方形纸板制成一副七巧板,将它拼成“小天鹅”图案,其中阴影部分的面积为________.
如图,用边长为1的正方形纸板制成一副七巧板,将它拼成“小天鹅”图案,其中阴影部分的面积为________. 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
20
| ||
| 3 |

| 2 |
| 3 |
| 6 |


查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
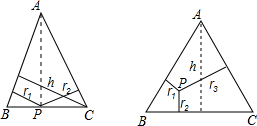
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•丹徒区模拟)用两个边长为1的正六边形拼接成如图(a)的图形,其周长为10;用三个边长为1的正六边形可以拼接成如图(b)或(c)的图形,其周长分别为12和14.若要拼接成周长为18的图形,所需这样的正六边形至少为x个,至多为y个,则x+y=
(2012•丹徒区模拟)用两个边长为1的正六边形拼接成如图(a)的图形,其周长为10;用三个边长为1的正六边形可以拼接成如图(b)或(c)的图形,其周长分别为12和14.若要拼接成周长为18的图形,所需这样的正六边形至少为x个,至多为y个,则x+y=查看答案和解析>>
科目:初中数学 来源: 题型:
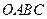 的顶点
的顶点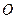 在坐标原点处,点
在坐标原点处,点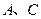 分别在
分别在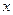 轴、
轴、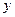 轴的正半轴上,点
轴的正半轴上,点 是
是 边上的点(不与点
边上的点(不与点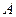 重合),
重合), ,且与正方形外角平分线
,且与正方形外角平分线 交于点
交于点 .
.
 坐标为
坐标为 时,试证明
时,试证明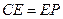 ;
; 坐标为(3,0)”改为“点
坐标为(3,0)”改为“点 坐标为(
坐标为( ,0)(
,0)(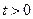 )”,结论
)”,结论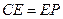 是否仍然成立,请说明理由;
是否仍然成立,请说明理由;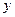 轴上是否存在点
轴上是否存在点 ,使得四边形
,使得四边形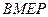 是平行四边形?若存在,用
是平行四边形?若存在,用 表示点
表示点
查看答案和解析>>
科目:初中数学 来源:2010年人教新课标初三模拟冲刺预测理科数学卷 题型:解答题
如图9,边长为5的正方形 的顶点
的顶点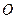 在坐标原点处,点
在坐标原点处,点 分别在
分别在 轴、
轴、 轴的正半轴上,点
轴的正半轴上,点 是
是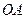 边上的点(不与点
边上的点(不与点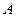 重合),
重合), ,且与正方形外角平分线
,且与正方形外角平分线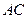 交于点
交于点 .
.
(1)当点 坐标为
坐标为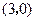 时,试证明
时,试证明 ;
;
(2)如果将上述条件“点 坐标为(3,0)”改为“点
坐标为(3,0)”改为“点 坐标为(
坐标为( ,0)(
,0)(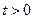 )”,结论
)”,结论 是否仍然成立,请说明理由;
是否仍然成立,请说明理由;
(3)在 轴上是否存在点
轴上是否存在点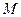 ,使得四边形
,使得四边形 是平行四边形?若存在,用
是平行四边形?若存在,用 表示点
表示点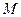
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com