Question

3．我们已经研究过函数的增减性（即单调性）、函数的对称性（即奇偶性）、函数的有界性，今天我们来研究一下函数的周期性．生活中有很多具有周期性的例子，如钟表的指针绕钟表圆心周而复始的旋转等，再如下面的例子：
甲乙两地开通了动车，设两地相距400千米，动车速度为200千米/时，若每隔2小时就有一辆动车从甲地发出，共有5辆动车，设第1辆动车出发的时刻为0时，第1辆动车出发时间为x小时，若设动车与乙地的距离为y₁千米，则上面描述可用下面的函数图象来表示（如图1）
其实，这五条线段可以用如下的函数解析式来表达：
y₁=-200（x-2i）+400（2i≤x≤2i+2，i=0，1，2，3，4）
（1）若在第一辆动车出发的同时，有一辆慢车从乙地开往甲地，速度为80千米/时，设慢车与乙地的距离为y₂千米，在图1 中画出这辆慢车运行的函数图象，并结合图象说明整个运行过程中，慢车与动车共相遇多少次？
（2）已知z=（x-1-2i）²（2i≤x≤2i+2，i=0，1，2，3）
①在图2的平面直角坐标系中画出这个函数的图象．
②当x=2.5和x=5.4时，对应的函数值分别为z₁和z₂，比较z₁和z₂的大小．
（3）若关于x的方程k（x+1）=（x-1-2i）²（2i≤x≤2i+2），i=0，1，2，3）有5个不相等的实数根，求k的取值范围．

Answer 1

分析 （1）根据路程=时间×速度列出函数的关系式，然后画出图形，最后根据图形找出交点的个数即可；
（2）①先根据i=0，1，2，3得到函数值的解析式，然后画出函数z的图象；②将当x=2.5和x=5.4分别代入函数的解析式，从而得到z₁和z₂的值，最后比较大小即可；
（3）方程有5个不相等的实数根，则函数y=k（x+1）与z=（x-1-2i）²（2i≤x≤2i+2，i=0，1，2，3）有5个不同的交点，从求得k的取值范围．

解答 解：（1）∵路程=时间×速度，
∴y₂=80x．
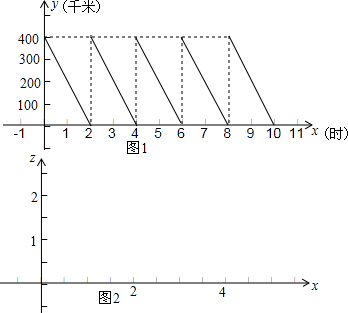
函数图象如图1所示：

∵函数y₁与y₂的图象有3个交点，
∴慢车与动车共相遇3次．
（2）①当i=0时，z=（x-1）²（0≤x≤2）；
当i=1时，z=（x-3）²（2≤x≤4）；
当i=2时，z=（x-5）²（4≤x≤6）；
当i=3时，z=（x-7）²（6≤x≤8）．
函数z=（x-1-2i）²（2i≤x≤2i+2，i=0，1，2，3）的图象如图所示：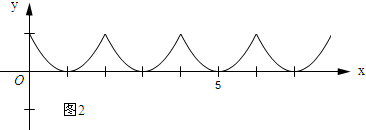

②将x=2.5代入z=（x-3）²（2≤x≤4）得：z₁=（2.5-3）²=0.25；
将x=5.4代入z=（x-5）²（4≤x≤6）得：z₂=（5.4-5）²=0.16．
∴z₁＞z₂．
（3）令y=k（x+1），
∵当x=-1时，y=0．
∴函数y=k（x+1）经过点（-1，0）．
当k=0时，函数y=k（x+1）的解析式为y=0．
∵函数Z=（x-1-2i）²（2i≤x≤2i+2），i=0，1，2，3）与x轴有5个交点，
∴k=0时，关于x的方程k（x+1）=（x-1-2i）²（2i≤x≤2i+2），i=0，1，2，3）有5个不相等的实数根．
如图3所示：直线y=k（x+1）与函数Z=（x-1-2i）²（2i≤x≤2i+2），i=0，1，2，3）有4个交点，且经过点（4，1）．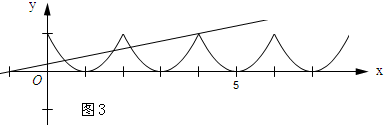

将x=4，y=1代入得；5k=1．
解得；k=$\frac{1}{5}$．
如图4所示；直线y=k（x+1）与函数Z=（x-1-2i）²（2i≤x≤2i+2），i=0，1，2，3）有6个交点，且经过点（6，1）．

将x=6，y=1代入得；7k=1．
解得；k=$\frac{1}{7}$．
∴当$\frac{1}{7}＜k＜\frac{1}{5}$时，关于x的方程k（x+1）=（x-1-2i）²（2i≤x≤2i+2），i=0，1，2，3）有5个不相等的实数根．
综上所述，当k=0或$\frac{1}{7}＜k＜\frac{1}{5}$时，方程有5个不相等的实数根．

点评 本题主要考查的是二次函数、一次函数的应用，解答本题的基本思路是将方程的根转化为两个函数图象的交点，数形结合是解题的关键．