
 如图,在矩形ABCD中,点E在CD边上,将矩形ABCD沿直线AE折叠,点D恰好落在BC边上的点F处.
如图,在矩形ABCD中,点E在CD边上,将矩形ABCD沿直线AE折叠,点D恰好落在BC边上的点F处.分析 (1)只要证明∠B=∠C=90°,∠AFB=∠FEC即可.
(2))因为△AFE是由△ADE翻折得到,推出AD=AF=5,EF=DE,设DE=EF=x,在Rt△ABF中,BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,推出FC=BC-BF=1,在Rt△EFC中,根据EF2=EC2+CF2,列出方程x2=(3-x)2+12解方程即可.
(3)只要证明∠FAE=∠DAE=∠BAF=30°,设ED=EF=a,则AD=$\sqrt{3}$a,EC=$\frac{1}{2}$a,求出AB、BC即可解决问题.
解答 解:(1)∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,AD=BC=5,AB=CD=3,
∵△AFE是由△ADE翻折得到,
∴∠AFE=∠D=90°,
∴∠AFB+∠EFC=90°,∠EFC+∠FEC=90°,
∴∠AFB=∠FEC,
∴△ABF∽△FCE.
(2)∵△AFE是由△ADE翻折得到,
∴AD=AF=5,EF=DE,设DE=EF=x,
在Rt△ABF中,BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴FC=BC-BF=1,
在Rt△EFC中,∵EF2=EC2+CF2,
∴x2=(3-x)2+12,
∴x=$\frac{5}{3}$.
(3)∵△FCE∽△AFE,△ABF∽△FCE,
∴∠EFC=∠FAE=∠BAF,
∵△AFE是由△ADE翻折得到,∠BAD=90°,
∴∠FAE=∠DAE=∠BAF=30°,设ED=EF=a,则AD=$\sqrt{3}$a,EC=$\frac{1}{2}$a,
∴AB=CD=$\frac{3}{2}$a,BC=AD=$\sqrt{3}$a,
∴$\frac{AB}{BC}$=$\frac{\frac{5}{2}a}{\sqrt{3}a}$=$\frac{5\sqrt{3}}{6}$.
∴$\frac{AB}{BC}$=$\frac{5\sqrt{3}}{6}$时,△FCE∽△AFE.
点评 本题考查相似三角形综合题、翻折变换、矩形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
| x | … | -3 | -2 | 1 | 2 | 3 | 4 | … |
| y | … | 12 | 5 | -4 | -3 | 0 | 5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
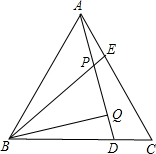 如图,已知△ABC是等边三角形,且AE=CD,AD、BE相交于P,BQ⊥AD于Q.
如图,已知△ABC是等边三角形,且AE=CD,AD、BE相交于P,BQ⊥AD于Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明和小亮用如图所示的两个转盘(每个转盘被分成三个面积相等的扇形)做游戏,转动两个转盘各一次,若两次数字之和为奇数,则小明胜;若两次数字之和为偶数,则小亮胜,这个游戏对双方公平吗?说说你的理由.
小明和小亮用如图所示的两个转盘(每个转盘被分成三个面积相等的扇形)做游戏,转动两个转盘各一次,若两次数字之和为奇数,则小明胜;若两次数字之和为偶数,则小亮胜,这个游戏对双方公平吗?说说你的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com