
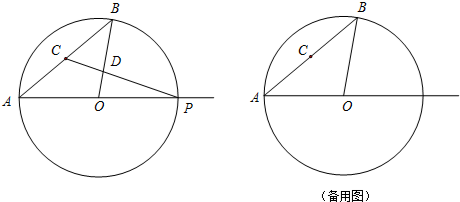
已知:⊙O的半径OA=5,弦AB=8,C是弦AB的中点,点P是射线AO上一点(与点A不重合),直线PC与射线BO交于点D.



(1)当点P在⊙O上,求OD的长.
(2)若点P在AO的延长线上,设OP=x,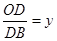 ,求y与x的函数关系式并写出自变量x 的取值范围。
,求y与x的函数关系式并写出自变量x 的取值范围。
(3)连接CO,若△PCO与△PCA相似,求此时BD的长。
解:当P在⊙O上时,连接BP
∵ C是AB中点,O是AP中点,
∴ 点D为△ABP的重心, ∴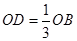
∵ OA=OB=5 ∴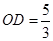
(2)过点O作OE//AB,交PC于点E(如图)
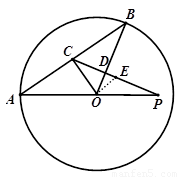
∵OE//AB ∴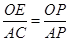 ,
, 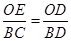
又∵ AC=BC ∴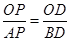
即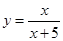 (x>0)
(x>0)
(3) 当P在AO延长线上时,若△PCO∽△PAC时,有∠PCO=∠A,
∵∠A=∠B,∴∠PCO=∠B, 易证△ACO∽△BDC
得 得
得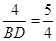 ∴
∴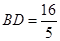
当P在AO上时,若△PCO∽△PAC时,可得CP⊥AO(如图)
作BH⊥AO,可求得 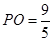 ,
,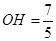
由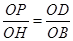 ,
得
,
得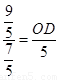 ∴
∴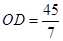
则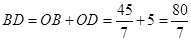
综上所述,若△PCO与△PCA相似,此时BD的长为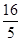 或
或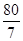
【解析】(1)连接BP,由两个中点得出点D是重心,可以得到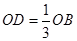 ;
;
(2)过点O作OE//AB,由三角形中线段的相似比找出y与x的函数关系式;
(3)考虑两种情况:点P在AO延长线上或者点P在AO上。


科目:初中数学 来源: 题型:
| OD | DB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com